Was ist die Szenariotechnik?

Bei einem Szenario handelt es sich um die Beschreibung möglicher Zukunftszustände bzw. um die potentielle Sequenz von Ereignissen. Die Entwicklung eines Szenarios erfolgt in mehreren Schritten, häufig unter Einsatz von Kreativitätstechniken.

Man beginnt mit der Festlegung des Untersuchungsfeldes (wie der Kapitalmarktentwicklung), danach erfolgt die Erfassung und Zuordnung der wichtigsten Einflussfaktoren auf den Untersuchungsgegenstand. Schließlich ermittelt man die Tendenzen der Entwicklung und stellt die kritischen Deskriptoren des Umfeldes heraus. Aus den Ergebnissen der vorherigen Schritte werden sogenannte Annahmebündel gebildet, die sich gegenläufig verhalten.

Die selbst gewählten Umfeldszenarien werden anschließend interpretiert und evaluiert. Darauf folgt eine Analyse, welche Auswirkungen auf bestimmte Szenarien durch potentielle Störereignisse hervorgerufen werden können. Die ermittelten Auswirkungen dienen dazu, die endgültige Szenarien-Darstellung vorzunehmen, respektive daraus abzuleiten, welche Konsequenzen Störereignisse auf das Untersuchungsfeld haben.

Um eine Maßnahmenkonzeption vorzunehmen, erfolgt eine Visualisierung der einzelnen Szenarien, oft in Form des sogenannten Szenario-Trichters (siehe hierzu Abbildung 3.9). In den meisten Fällen beschränkt man sich dabei auf zwei Extrem-Szenarien und zwei bis drei weitere. Die Komplexität und Anzahl der Szenarien erhöht sich umso mehr, je weiter der betrachtete Zeitraum in die Zukunft reicht. 

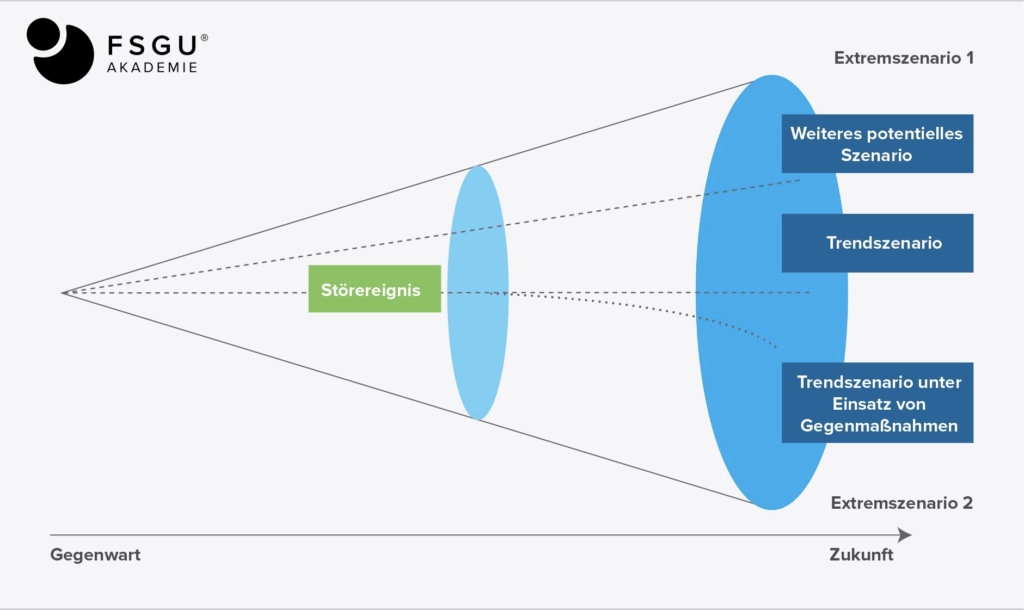
Bei den abgeleiteten Szenarien handelt es sich um die Konstellation möglicher Ausprägungen.

Ein wesentliches Element des Szenarios ist die Cross Impact-Matrix: Diese gibt Auskunft darüber, wie gut zwei Ausprägungen unterschiedlicher Deskriptoren zusammenpassen. Die Cross Impact Matrix wird auch Wechselwirkungsmatrix genannt und stellt eine hoch komplexe Methode zur Erstellung und Beurteilung von Szenarien mit vielen, analytisch nicht beschreibbaren Faktoren dar. Analog zur Delphi-Methode basiert sie auf Experteneinschätzungen.

Exkurs: Was ist die Delphi-Methode?

Bei der Delphi-Methode erfolgt eine Befragung von Fachexperten über mehrere (häufig drei) Runden. Mittels dieser Methode soll ein Konsens gefunden werden, der für alle an der Entscheidungsfindung Beteiligten tragbar ist. Ein entscheidender Faktor ist Anonymität, die dazu führt, dass nicht beabsichtigte Beeinflussungen durch andere Meinungen ausbleiben und die Beteiligten ihre eigenen Ansichten im Verlauf des Verfahrens überdenken und bei Bedarf abändern können. Nachfolgend der exemplarische Ablauf eines Entscheidungsfindungsverfahrens mit der Delphi-Methode:

Das Delphi-Team besteht aus Betriebsangehörigen. Falls notwendig werden externe Teilnehmer hinzugezogen. Das Team formuliert die exakten Fragestellungen bzw. diskutiert, welche Fragen im Untersuchungskontext relevant sind. Anschließend werden Experten benannt, die die Prognoseproblematik aus unterschiedlichsten Perspektiven beleuchten sollen. Daraufhin erfolgt der erste Umlauf der Befragung. Diese wird nach dem Rücklauf vom Delphi-Team ausgewertet. 

Hierbei werden auch statistische Kenngrößen (Median, Mittelwert, minimale bzw. maximale Prognose) und der Quartilsabstand (inneres Intervall aller Prognosen, in das 50% der Schätzungen fallen) gebildet. Nach der Veröffentlichung der Ergebnisse an die Experten beginnt die nächste Befragung. Sollte ein Teilnehmer seine Meinung ändern, ist eine Begründung hierfür erforderlich. Nach dem Rücklauf kommt es wiederum zur Auswertung mit Bekanntgabe der Ergebnisse und es folgt die dritte und letzte Befragung. Nach dem Rücklauf erfolgt die finale Auswertung und Prognose. Beispielhaft kann z.B. die Quartilsspanne als mögliches Prognosespektrum oder der Median als Einpunktprognose festgelegt werden.

Bei der Cross Impact Matrix (CIM) erfolgt eine Faktorengegenüberstellung (hauptsächlich Ereignisse) in einer Matrix. In den Zeilen werden die betrachteten Ursachen, in den Spalten die möglichen Wirkungen eingetragen. Wechselwirkungen können nur erfasst werden, wenn in der originalen CIM alle Faktoren sowohl als Ursachen als auch als Wirkungen aufgeführt sind.

An den Kreuzungspunkten vermerken die Experten unabhängig voneinander ihre Einschätzung des Einflusses der einzelnen Ursachen auf die benannte Wirkung. Dies kann mittels einfacher Bewertungskriterien (großer Einfluss, kein Einfluss, negativer Einfluss) oder in Zahlenskalen erfolgen. Aus den separaten Ergebnissen wird dann eine gemeinsame Matrix erstellt und wiederum den Experten zur Evaluierung vorgelegt.

Zweck der CIM ist die Beurteilung der Eintrittswahrscheinlichkeit verschiedener möglicher Zukunftsszenarios (diese werden als „Futuribles“ bezeichnet). Sie hat beschreibenden Charakter und soll der Orientierung dienen.

Da manuell die komplexen Rückwirkungen nicht hinreichend erfasst werden können, ist der Einsatz einer Simulations-Software nahezu unabdingbar.

Einsatzmöglichkeiten der CIM liegen in volkswirtschaftlichen Zusammenhängen, sie eignet sich aber auch zur Erstellung von Businessplänen oder zur Risikoanalyse.

Ereignis	E1	E2	E3
E1	–	E1 ist zwingende Voraussetzung für E2	E1 erhöht Eintrittswahrscheinlichkeit für E3
E2	E2 kann nicht vor E1 auftreten, beeinflusst nicht den Verlauf von E1	–	E2 verstärkt E3 bei unveränderter Eintrittswahrscheinlichkeit
E3	Keine Beziehung	Keine Beziehung	–
E4	Keine Beziehung	E4 reduziert Wirkung von E2	E4 reduziert Eintrittswahrscheinlichkeit von E3

Ereignis	Rückgang des Ölverbrauchs	Lockerung des OPEC-Kartells (Preissenkung)	Wirtschaftliche Nutzbarkeit von Windkraftwerken
Rückgang des Ölverbrauchs	abschwächend, verzögernd	verstärkend, beschleunigend	abschwächend, verzögernd
Lockerung des OPEC-Kartells (Preissenkung)	verstärkend, beschleunigend	–	abschwächend, verzögernd
Wirtschaftliche Nutzbarkeit von Windkraftwerken	Keine Beziehung	verstärkend beschleunigend

Was ist eine einfache Konsistenzanalyse?

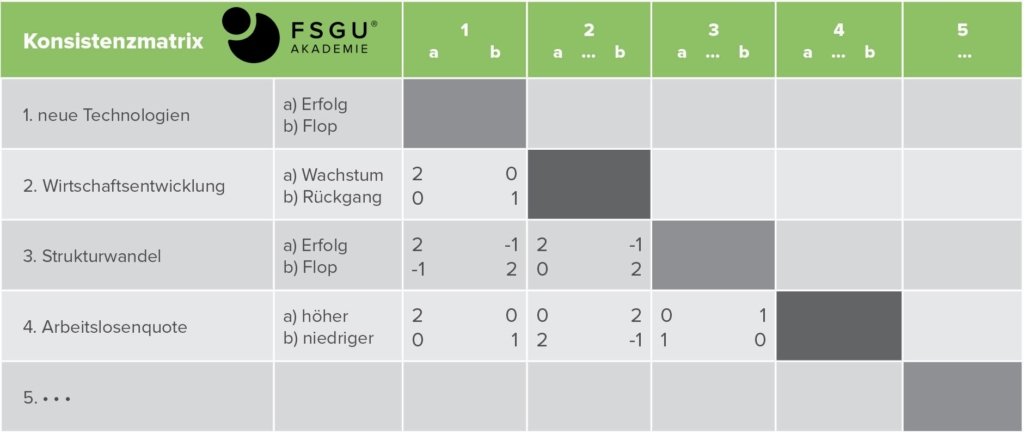
Das Ziel der einfachen Konsistenzanalyse als Form der Cross Impact-Matrix ist, Szenarien herauszufinden, die in sich konsistent sind. Es passen alle Ausprägungen zusammen und es erfolgt keine Wahrscheinlichkeitsanalyse. Zwingend notwendig für den Dateninput ist eine Konsistenz-Matrix. Darin enthalten sind bestimmte Kennzahlen von 1 (Ausprägungen passen gar nicht zusammen) bis 5 (Ausprägungen passen bestens zusammen).

Genaue Maßstäbe, wann ein Szenario als konsistent anzusehen ist (beispielsweise Mindestwert von 2), existieren nicht.

Die Konsistenzanalyse kann lediglich dabei unterstützen, die Gesamtzahl der Szenarien durch individuelle Beschränkungen zu reduzieren und ist als Hilfestellung zur Herstellung von Übersichtlichkeit zu betrachten.

Was ist ein Symmetrischer Cross Impacts?

Bei den symmetrischen Cross Impacts geht es um die Einführung von Szenariowahrscheinlichkeiten.

Sie sind ein subjektives Maß des Anwenders, das aufzeigt, wie groß aus seiner Sicht die Wahrscheinlichkeit der jeweiligen Ausprägungen ohne Berücksichtigung von Wechselwirkungen mit anderen Deskriptorenausprägungen ist.

Symmetrische Cross Impacts existieren, sobald es für je zwei Ausprägungen (unterschiedlicher Deskriptoren) nur genau eine Konsistenzzahl gibt. Systemgrößen bzw. Ausprägungen werden in vier Bereiche eingeteilt: Eingriffs-, Rahmen-, Aktiv- und Passivgrößen.

Zum besseren Verständnis der Begriffsdefinition ist in der nachfolgenden Abbildung die Wechselwirkung in vernetzten Systemen exemplarisch dargestellt.

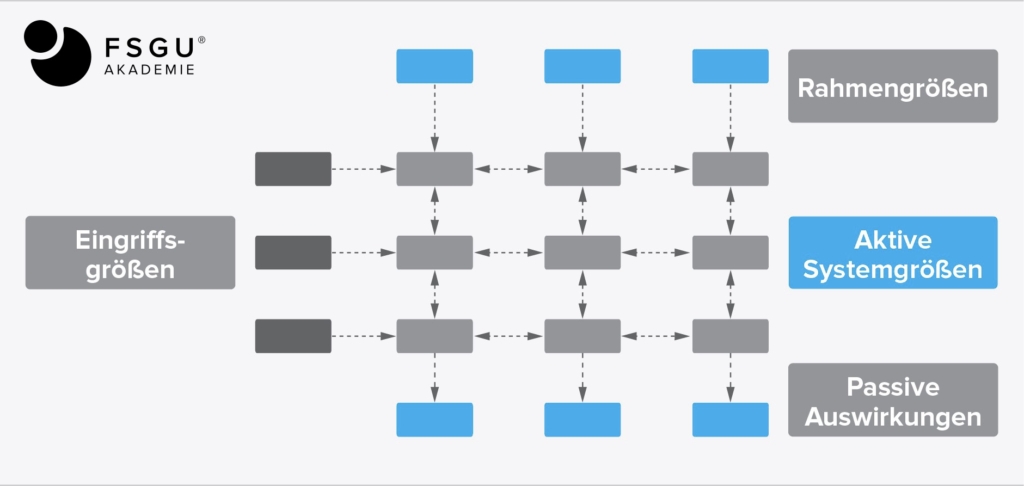
Die Unterteilung in vier Bereiche erfolgt, damit bei einer umfangreichen Anzahl von Systemgrößen das Verfahren handhabbar bleibt. Die vier Bereiche sind wie folgt charakterisiert:

• Eingriffsgrößen wirken von außen auf das System, ohne dass eine Rückkopplung vom System auf diese wirkt. Dies geschieht in Form vorgegebener Interventionen, die dann eingesetzt werden, wenn die Reaktionen des Systems auf Eingriffe zur Durchsetzung bestimmter Entwicklungen untersucht werden sollen.
• Rahmengrößen haben auf aktive und passive Systemgrößen Einfluss, erfahren aber selbst keine Beeinflussung durch diese. Für die Szenarioanalyse können sie als vorbestimmte, extern bedingte Größen beschrieben und festgelegt werden.
• Aktive Systemgrößen beeinflussen die Passivgrößen und bewirken wechselseitige Einflüsse untereinander.
• Passive Auswirkungen können durch Eingriffs-, Rahmen- und aktive Systemgrößen beeinflusst werden. Eine Rückwirkung auf die genannten Bereiche findet nicht statt. Innerhalb der Passivgrößen können allerdings Wechselwirkungen auftreten.

Durch diese obige Charakterisierung wird die Bearbeitung der Cross Impact-Matrix vereinfacht, da hierdurch die wechselseitige Beeinflussung der Systemgrößen in bestimmten Teilbereichen entfällt. Die Rahmengrößen können auch komplett aus der CI-Matrix herausgenommen werden, da ihre Entwicklung innerhalb der möglichen Szenarien schon bekannt ist. Die potentiellen Zustände der Systemgrößen („Deskriptoren“) werden, soweit es sich um kontinuierliche Quantitäten handelt, in Intervallen zusammengefasst und als Deskriptorenausprägungen geführt.

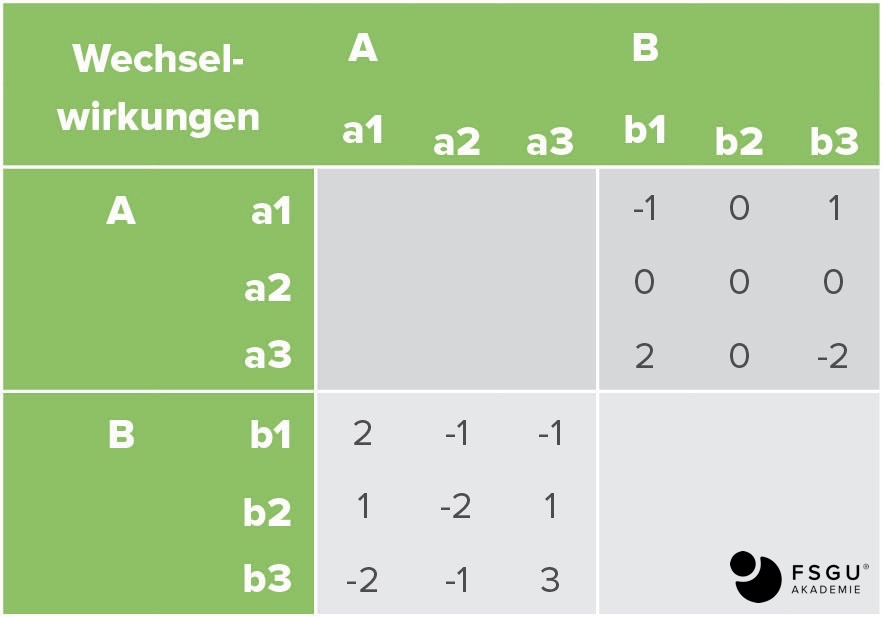
Durch die Festlegung der Deskriptorenliste und ihrer Ausprägungen ist auch die Gesamtzahl der kombinatorisch möglichen Szenarien gegeben. Bei der Anwendung des Verfahrens im Rahmen von MEX III (hier wurde von 2002 bis 2003 die Rolle der erneuerbaren Energien in der deutschen Stromwirtschaft untersucht) setzte sich die Cross-Impact-Matrix beispielsweise aus vier Deskriptoren mit zwei Ausprägungen, fünf Deskriptoren mit drei Ausprägungen und fünf Deskriptoren mit vier Ausprägungen zusammen. Somit ergaben sich kombinatorisch 2⁴*3⁵*4⁵=3.981.312 verschiedene Deskriptorenkonstellationen. Bei einem realen System sind diese nicht alle relevant, da die meisten von ihnen teils sinnlose Kombinationen von Deskriptorenausprägungen darstellen. Mithilfe eines Computerprogramms wurden alle Deskriptorenkonstellationen geprüft. Damit werden die wenigen Deskriptorenkonstellationen (Szenarien) aus der Menge der kombinatorischen Möglichkeiten herausgefiltert, die mit der in der Cross-Impact-Matrix formulierten Systembeschreibung konsistent sind.

Zur Ermittlung von Szenariowahrscheinlichkeiten geht man wie folgt vor:

1. Ermittlung oberer und unterer Intervallgrenzen für die gemeinsamen Wahrscheinlichkeiten p(i,j) der beiden Ausprägungen i und j unterschiedlicher Deskriptoren.
2. Festlegung vorläufiger gemeinsamer Wahrscheinlichkeiten p(i,j) aus den ermittelten Intervallgrenzen und den im Ausgangstableau gegebenen Cross Impacts CI (i,j).
3. Modifikation der vorläufigen gemeinsamen Wahrscheinlichkeiten in endgültige Wahrscheinlichkeiten p*(i,j), die den Wahrscheinlichkeitsaxiomen genügen, und Berechnung der Szenariowahrscheinlichkeiten.

Bei mehr als zwei Deskriptoren muss der Ansatz der linearen Programmierung verwendet werden, um an die Szenariowahrscheinlichkeiten zu gelangen.

Die vorgestellten Szenarioanalyseverfahren sind hilfreiche Mittel bei einer fundierten strategischen Prognoseplanung und beschränken sich nicht darauf, einfach Trends fortzuschreiben, sondern führen zur Gewinnung völlig neuer Zukunftsbilder.

Damit kann die Szenarioanalyse auch als mittelbar unterstützendes Instrument in der Alternativensuche im Sinne einer langfristigen Strategieplanung betrachtet werden.

Die Entscheidung für die jeweilige Methode ist abhängig vom akzeptierten Aufwand sowie den Wahrscheinlichkeiten innerhalb der Analyse.

Die in den vorherigen Punkten genannten Techniken und Methoden dienen als Grundlage für die Identifizierung zentraler Handlungsfelder und die Festlegung der strategischen Ausrichtung.

CI-Verfahren sind grundsätzlich kein exaktes Berechnungsverfahren, sondern lediglich eine strukturierte Methode, um eigene Systemeinschätzungen zu reflektieren. Es ist geeignet für die qualitativ orientierte Bearbeitung komplexer Systeme, deren Wechselwirkungen man nicht unmittelbar durchschauen kann. Durch das Verfahren kann eine rationale, systematische und nachvollziehbare Erzeugung konsistenter Szenarien aus Wechselbeziehungs-Einschätzungen und der vollständigen Überprüfung der kombinatorischen Möglichkeitsvielfalt vorgenommen werden. Es bietet zudem Chancen für den Umgang mit Expertengruppen, die heterogene Systemeinschätzungen vorgenommen haben.

Der weitere Vorteil des Verfahrens liegt in der einfachen Nachprüfbarkeit der Auswertungsprozedur für alle, die daran beteiligt sind. Die Prüfung von im Einzelfall Millionen von Szenarien muss rechnergestützt erfolgen, die Konsistenz der resultierenden Szenarien oder eigener, intuitiv erstellter Szenarien kann aber von allen überprüft und nachvollzogen werden.