Was ist ein Datenbankschemata?

E.F. Codd hat zwölf Regeln für RDBMS (relationale Datenbankmanagementsysteme) aufgestellt:

1. Informationsregel: Alle Informationen in einer relationalen Datenbank (einschl. Bezeichnern von Tabellen und Spalten) sind explizit als Datenwerte in Tabellen darzustellen.
2. Garantierter Zugriff auf Daten: Jeder Datenwert einer relationalen Datenbank muss durch eine Kombination von Tabellenbezeichner, Primärschlüssel und Spaltenbezeichner auffindbar sein.
3. Systematische Behandlung von Nullwerten: Das DBMS behandelt Nullwerte durchgängig gleich als unbekannte oder fehlende Werte und unterscheidet diese von Standardwerten.
4. Struktur einer Datenbank: Eine Datenbank und ihre Inhalte werden in einem Systemkatalog auf derselben logischen Ebene wie die Daten selbst, also in Tabellen gehalten. Der Katalog lässt sich also mit einer Datenbanksprache abfragen.
5. Abfragesprache: Zu einem relationalen Datenbanksystem gehört eine Abfragesprache mit einem vollständigen Befehlssatz für die Datendefinition, Manipulation, Integritätsregeln, Autorisierung und Transaktionen.
6. Aktualisieren von Sichten: Alle Sichten, die theoretisch aktualisiert werden können, lassen sich auch vom System aktualisieren.
7. Abfragen und Bearbeiten ganzer Tabellen: Das DBMS unterstützt nicht nur Abfragen, sondern auch Operationen für das Einfügen, Modifizieren und Löschen.
8. Physikalische Datenunabhängigkeit: Der logische Zugriff auf Daten muss unabhängig von den physikalischen Zugriffsmethoden sein.
9. Logische Datenunabhängigkeit: Änderungen der Tabellenstrukturen dürfen keinen Einfluss auf die Logik der Anwendungsprogramme haben.
10. Unabhängigkeit der Integrität: Integritätsregeln müssen sich in der Datenbanksprache definieren lassen. Sie werden im Systemkatalog gespeichert. Sie können nicht umgangen werden.
11. Verteilungsunabhängigkeit: Der Zugriff von Anwendungen auf die Daten darf sich nicht beim Übergang von einem unverteilten zu einem verteilten System ändern.
12. Kein Unterlaufen der Abfragesprache: Integritätsregeln, die mit der Abfragesprache definiert wurden, dürfen sich nicht durch eine Low-Level-Sprache umgehen lassen.

Relationenschema

Ein Relationenschema wird wie folgt bezeichnet:

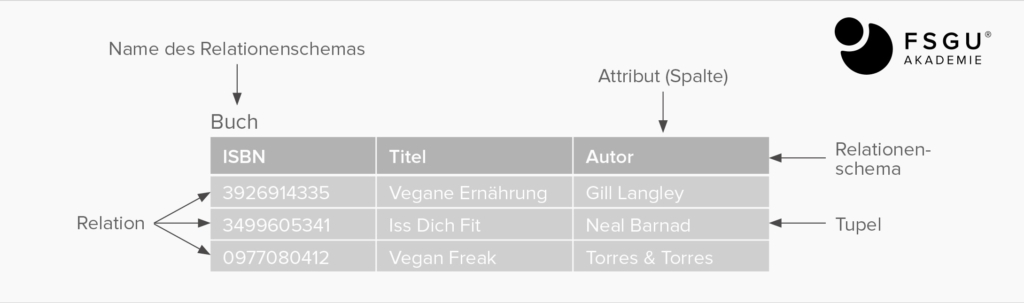
Domänen

Domänen stellen einen Wertebereich für Attribute zur Verfügung. Eine Domäne hat einen eindeutigen Bezeichner. Die Werte des Wertebereichs einer Domäne müssen atomar sein. Eine Relation im Relationenmodell ist eine Relation der Wertebereiche von Domänen.

Ein relationales Datenbanksystem stellt einen Vorrat an vordefinierten Domänen zur Verfügung, beispielsweise

• Numerische Datentypen:
  • Ganzzahltypen
  • Festkommatypen
  • Gleitkommatypen
  • Datum
  • Zeit
• Alphanumerische Datentypen:
  • Character (einzelne Zeichen)
  • Zeichenketten mit fester Länge
  • Zeichenketten mit variabler Länge
• Binäre Datentypen:
  • Bitfolgen mit fester Länge
  • Bitfolgen mit variabler Länge

Des Weiteren ist es möglich, eigene Domänen zu definieren. Dieses geschieht durch Einschränken vorhandener Domänen, d.h. es können Teilmengen definiert werden. Beispielsweise kann eine Postleitzahl als ganze Zahl oder Text mit fester Länge definiert werden. 

Präziser kann eine Postleitzahl aber durch eine geeignete Teilmenge beschrieben werden, womit das Einfügen falscher Werte besser zurückgewiesen werden kann – dies wird als Domänenintegrität (siehe unten) bezeichnet.

Schlüsselkandidat

Da Relationen Elemente einer Menge sind, sind sie wohl unterschieden. Dann gibt es aber auch eine minimale Anzahl an Attributen, in denen sie sich unterscheiden.

Ein Schlüsselkandidat besteht aus einem oder mehreren Attributen einer Relation:

• Es gibt keine zwei Tupel mit denselben Attributswerten des Schlüsselkandidaten
• Ein Schlüsselkandidat ist minimal mit dieser Eigenschaft, d. h. es werden alle Attribute des Schlüsselkandidaten zur Identifizierung benötigt

Primärschlüssel

Jede Relation muss einen Primärschlüssel besitzen. Er ist aus der Menge der Schlüsselkandidaten auszuwählen. Im Allgemeinen ist derjenige Schlüsselkandidat am geeignetsten, der eine minimale Anzahl an Attributen hat. 

Mit Hilfe von Primärschlüsseln werden Beziehungen definiert. Dabei entsteht zwangsläufig eine gewisse Datenredundanz. Je kleiner der Primärschlüssel ist, desto geringer ist auch die Datenredundanz. Eine weitere wichtige Aufgabe eines Primärschlüssels ist das zeitlich schnelle Auffinden von Datensätzen. Auch hier gilt: je kleiner der Primärschlüssel, desto performanter können Datensätze gefunden werden.

Um den Minimalanforderungen gerecht zu werden, kann ein Surrogatschlüssel, d.h. ein künstlicher Schlüssel, definiert werden. Er besteht meist aus einer fortlaufenden Nummer.

Fremdschlüssel

Beziehungen von Relationen werden durch Fremdschlüssel ausgedrückt. Ein Fremdschlüssel ist eine Menge von Attributen einer Relation, der in einer anderen oder in der gleichen Relation ein Primärschlüssel zugeordnet ist. Einer Relation mit einem Fremdschlüssel wird dadurch eindeutig eine Relation mit dem entsprechenden Primärschlüssel zugeordnet. 

Die Attribute des Fremd- und des Primärschlüssels müssen verträglich sein, d. h.  entsprechende Attribute müssen die gleiche Domäne haben, sie können sich aber im Namen unterscheiden.

Einige wichtige Eigenschaften von Fremdschlüsseln:

• Zu jedem Zeitpunkt müssen zu den Werten eines Fremdschlüssels die gleichen Werte des korrespondierenden Primärschlüssels existieren.
• Attribute eines Fremdschlüssels dürfen NULL-Werte haben, wenn sie nicht zugleich Attribute eines Primärschlüssels sind.
• Die Attribute eines Fremdschlüssels müssen mit den korrespondierenden Attributen des Primärschlüssels verträglich sein.
• Eine Relation kann mehrere Fremdschlüssel haben, und damit zu mehreren Relationen in Beziehung stehen.
• Eine Relation kann auf sich selbst referenzieren.

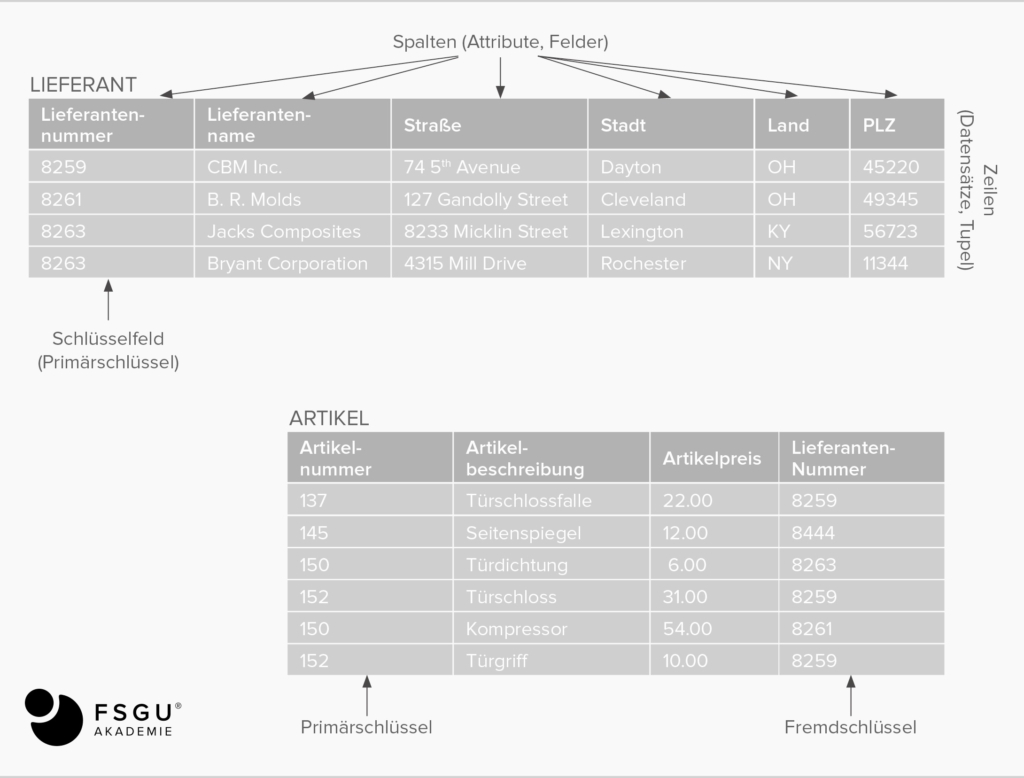
Relationale Integrität

An Relationen bzw. an ihre Attribute werden Bedingungen geknüpft. Die Integritätsregeln sollen die Konsistenz mit den Bedingungen gewährleisten. Diese Bedingungen nennt man auch Integritätsbedingungen.

Es werden vier Integritätsregeln unterschieden:

• Domänenintegrität
• Entitätsintegrität
• Referenzielle Integrität
• Intrarelationale Integrität

1.) Domänenintegrität

Die Attributwerte der Relationen dürfen ausschließlich Werte der Domäne annehmen.

2.) Entitätsintegrität

Jedes Tupel ist eindeutig durch den Primärschlüssel identifizierbar. Entitätsintegrität wird auch Eindeutigkeitsintegrität genannt. Daraus folgt, dass ein Primärschlüssel keine NULL-Werte enthalten darf.

3.) Referentielle Integrität

Für jeden Fremdschlüssel gilt:

• Alle Attribute eines Fremdschlüssels sind entweder ungleich NULL oder alle sind gleich NULL. Im ersten Fall ist der Fremdschlüssel vollständig definiert, im zweiten Fall ist er vollständig annulliert.
• Für einen vollständig definierten Fremdschlüssel muss in der durch den Fremdschlüssel referenzierten Relation ein Tupel existieren, dessen Primärschlüssel identisch mit dem Fremdschlüssel ist.

Die referentielle Integrität wirkt sich auf das Löschen und das Einfügen von Datensätzen aus. Beide Operationen können die referentielle Integrität verletzen.

Wird ein Datensatz gelöscht, so dürfen keine Fremdschlüsselverweise mehr auf diesen Datensatz zeigen. Wenn dies doch der Fall ist, dann kann das Datenbanksystem auf unterschiedliche Weisen reagieren:

• Der geplante Löschvorgang wird von dem Datenbanksystem verweigert.
• Es werden auch alle Datensätze gelöscht, die auf den zu löschenden Datensatz verweisen. Bei mehrfachen Abhängigkeiten kann so eine sehr aufwendige Löschoperation entstehen.
• Die Attribute der Fremdschlüssel, die auf den zu löschenden Datensatz verweisen, werden auf NULL gesetzt, wenn das möglich ist.

Wenn ein Datensatz eingefügt wird, dessen Fremdschlüssel keinem Primärschlüssel entspricht, sollte er abgewiesen werden.

4.) Intrarelationale Integrität (zusätzliche Regeln)

Es können zusätzliche Regeln (engl.: constraint = Einschränkung, Bedingung) definiert werden. Diese können sich auf ein einzelnes Attribut der Relation oder auch auf mehrere Attribute beziehen. So kann beispielsweise gefordert werden, dass auch ein Nichtschlüsselattribut eindeutig zu sein hat, oder dass etwa ein Anfangsdatum vor einem Enddatum zu liegen hat.

Anomalien

Schlecht entworfene Relationenschemata können zu Anomalien führen. Anomalien entstehen aufgrund redundant gespeicherter Informationen. Sie bewirken aufgrund der Redundanz zusätzliche Operationen im Datenbankbetrieb und können zudem die Integrität der Daten einer Datenbank verletzen.

Ursachen für einen schlechten semantischen DB-Entwurf sind typisch

• Kein semantischer DB-Entwurf und direkte Modellierung im relationalen Modell
• Fehlerhafte Optimierung von Beziehungen 
• Versuchte Zugriffsoptimierung durch Zusammenlegen von Informationen mehrerer Tabellen, um Joins einzusparen
• Funktionalitätserweiterungen durch neue Anforderungen im laufenden Datenbankbetrieb

Es werden drei Arten von Anomalien unterschieden: Einfügeanomalien, Updateanomalien und Löschanomalien.

A) Einfügeanomalien

Werden beispielsweise neben Nummer und Titel einer Lehrveranstaltung gleichzeitig noch die Informationen Personalnummer und der Name der jeweiligen Lehrkraft direkt in der Tabelle Lehrveranstaltung gespeichert würde dies wie folgt aussehen:

	Lehrveranstaltung
Nummer	Titel	PersNr.	Name
123	Datenstrukturen	6897	Dr. Seifert
234	Datenbanken in der Praxis	6897	Dr. Seifert
345	Datenbanken Grundlagen	6123	Prof. Benn
456	Übung Datenstrukturen	6897	Dr. Seifert

Mit dieser Ausgangssituation soll nun eine neue Vorlesung „Mathematik für Ingenieure“ mit der Nummer 512 angeboten werden. Allerdings ist im Moment noch nicht klar, welche Lehrkraft die neue Lehrveranstaltung durchführt, deshalb müssen PersNr und Name mit Nullwerten aufgefüllt werden:

	Lehrveranstaltung
Nummer	Titel	PersNr.	Name
123	Datenstrukturen	6897	Dr. Seifert
234	Datenbanken in der Praxis	6897	Dr. Seifert
345	Datenbanken Grundlagen	6123	Prof. Benn
456	Übung Datenstrukturen	6897	Dr. Seifert
512	Mathematik für Ingenieure	null	null

Als nächste Aktion soll eine neue Lehrkraft namens Dr. Zimmer mit der PersNr 7856 eingefügt werden:

	Lehrveranstaltung
Nummer	Titel	PersNr.	Name
123	Datenstrukturen	6897	Dr. Seifert
234	Datenbanken in der Praxis	6897	Dr. Seifert
345	Datenbanken Grundlagen	6123	Prof. Benn
456	Übung Datenstrukturen	6897	Dr. Seifert
null	null	7856	Dr. Zimmer

Analog der vorhergehenden Aktion müssten jetzt die Attribute Titel und Nummer mit Nullwerten aufgefüllt werden. Allerdings ist die Nummer der Lehrveranstaltung der Schlüssel der Tabelle Lehrveranstaltung und kann demzufolge keine Nullwerte annehmen. Folglich ist die Einfügeanomalie in diesem Beispiel eklatant und verhindert das Einfügen des neuen Tupels vollständig.

Allgemein tritt die Einfügeanomalie auf, wenn in einer Tabelle Informationen mehrerer Entity-Typen (siehe 2.2 Entity-Relationship-Modell – Begriffe und Darstellung) miteinander vermischt worden sind. Möchte man Informationen eintragen, die nur zu einem Entity-Typ gehören, kommt es zu Problemen.

B) Updateanomalie

Angenommen, dass Dr. Seifert in das Büro 1/336h umziehen soll

	Lehrveranstaltung
Nummer	Titel	PersNr.	Name	Büro
123	Datenstrukturen	6897	Dr. Seifert	1 / 336g
234	Datenbanken in der Praxis	6897	Dr. Seifert	1 / 336g
345	Datenbanken Grundlagen	6123	Prof. Benn	1 / 336g
456	Übung Datenstrukturen	6897	Dr. Seifert	1 / 336g

müssten die vorhandenen Einträge in der Tabelle z.B. mit folgendem SQL-Statement gelöscht werden:

DELETE
  FROM Lehrveranstaltung
  WHERE PersNr = 6897

Die Updateanomalie oder auch Änderungsanomalie beschreibt nun die Notwendigkeit, die gleiche Änderung an verschiedenen Tupeln vollziehen zu müssen. Dadurch ergeben sich ein erhöhter Speicherbedarf wegen redundant gespeicherter Informationen, Leistungseinbußen bei Änderungen aufgrund mehrfacher Änderungsoperationen und wegen der redundanten Speicherung von Informationen besteht die potentielle Gefahr, dass ein oder mehrere Tupel bei der Änderung „vergessen“ werden und die Datenbank dadurch inkonsistent wird.

C) Löschanomalie

Aus der Tabelle soll die Lehrveranstaltung „Datenbanken Grundlagen“ wegen Wegfall gelöscht werden:

	Lehrveranstaltung
Nummer	Titel	PersNr.	Name	Büro
123	Datenstrukturen	6897	Dr. Seifert	1 / 336g
234	Datenbanken in der Praxis	6897	Dr. Seifert	1 / 336g
345	Datenbanken Grundlagen	6123	Prof. Benn	1 / 336g
456	Übung Datenstrukturen	6897	Dr. Seifert	1 / 336g

Das zugehörige SQL-Statement könnte wie folgt aussehen:

DELETE
  FROM Lehrveranstaltung
  WHERE Nummer = 345

Das Problem dabei ist, dass das Löschen der Lehrveranstaltung „Datenbanken Grundlagen“ auch alle Informationen der Lehrkraft entfernt.

Allgemein tritt die Löschanomalie auf, wenn in einer Tabelle Informationen mehrerer Entity-Typen miteinander vermischt worden sind. Möchte man Informationen löschen, die nur einen Entity-Typ betreffen, werden (oft unbeabsichtigt) auch die Informationen von anderen Entities gelöscht.

Relationale Algebra 

Nach (Rausch, 1999): E. F. Codd definierte eine vollständige Syntax auf 8 Operatoren und schuf eine relationale Algebra. Er zeigte, dass damit alle denkbaren Zugriffe auf beliebige Relationen der Datenbank möglich sind.

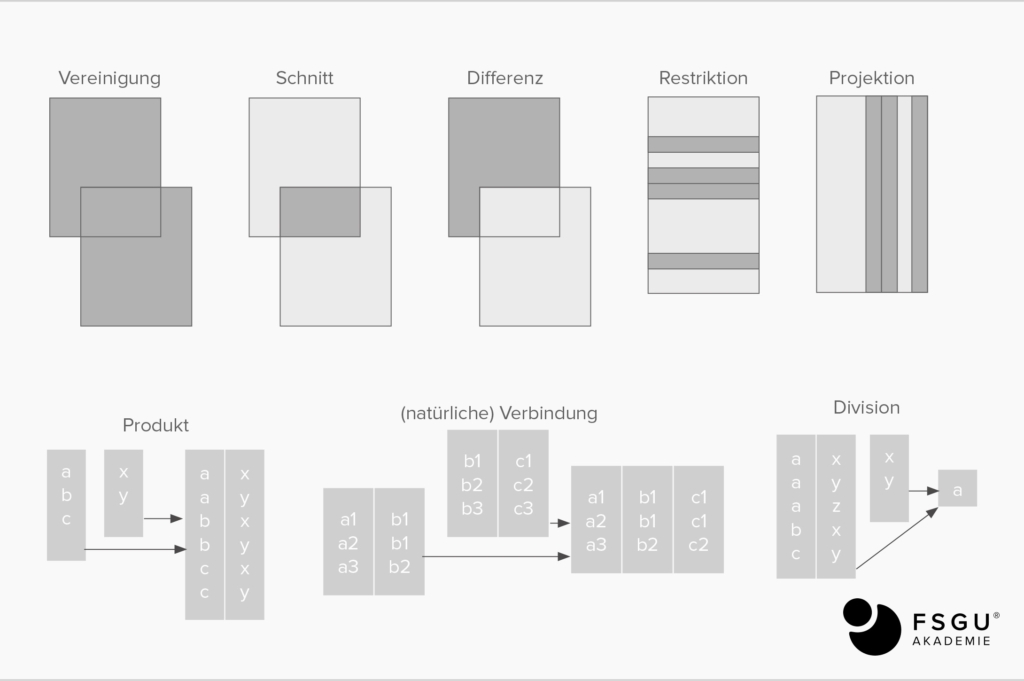
Es gibt 8 Mengenoperatoren auf R x R (binäre Operatoren) und R (unäre Operatoren). Das Bildgebiet ist wieder eine Menge (Relation). Binäre Operatoren sind z.B. Addition und Multiplikation, unäre Operatoren sind z.B. das negative Vorzeichen.

Vereinigung: R1 UNION R2

Ergibt alle Tupel, die wenigstens in einer der beiden Relationen vorkommen.
Input: zwei Relationen R1, R2 gleicher Struktur
Output: Vereinigungsmenge der Tupel/Zeilen der beiden Relationen

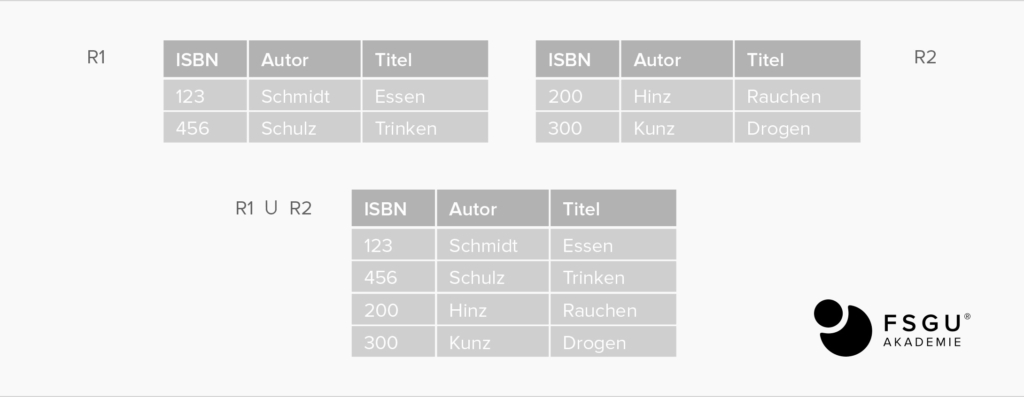
Schnitt: R1 INTERSECT R2
Enthält nur die in beiden Relationen vorkommenden Tupel.

Differenz: R1 MINUS R2

Bezüglich der Tupel: R1 ohne R2, d.h. R1 R2
Input: zwei Relationen R1, R2 gleicher Struktur
Output: alle Tupel/Zeilen aus R1, die nicht in R2 enthalten sind

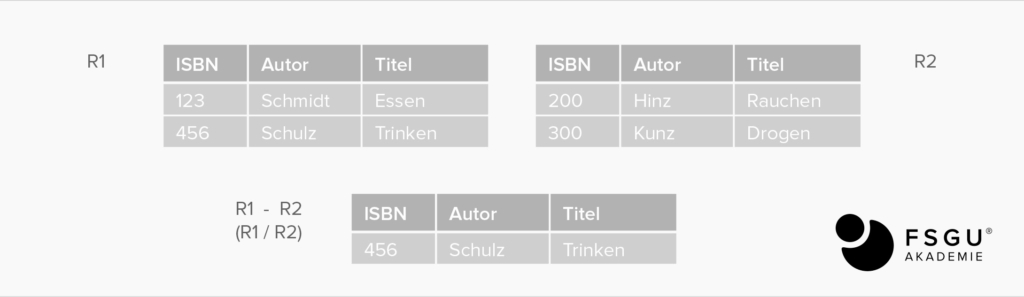
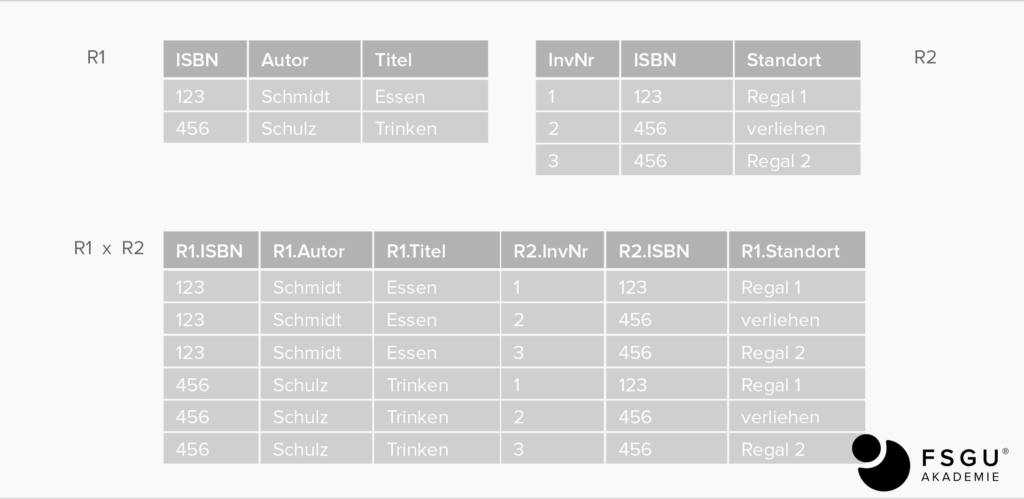
Kartesisches Produkt: R1 TIMES R2

alle möglichen Kombinationen der Tupel aus R1 und R2.

Input: 2 beliebige Relationen R1 und R2
Output: alle Tupel, die sich als Kombination von einem Tupel aus R1 und einem Tupel aus R2 ergeben

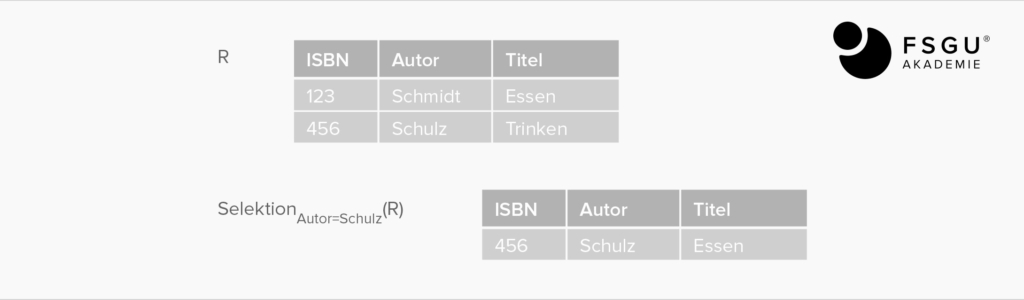
Restriktion (Selektion): R WHERE Bedingung

die sich ergebende Relation ist eine Teilmenge von R entsprechend der Bedingung.

Selektionsbedingungen können sein

• Vergleichsoperatoren <, ≤, >, ≥, =, ≠
• Boolesche Ausdrücke ∩ (UND), ∪ (ODER), ¬ (NOT) und Klammern

Input: eine beliebige Relation R
Output: Relation R unter Einschränkung auf solche Tupel/Zeilen, die eine bestimmte Bedingung erfüllen

Projektion: R [Attributsauswahl]
alle Tupel, aber nur mit einer Auswahl von Attributen werden angezeigt.
Input: eine beliebige Relation
Output: Relation R unter Einschränkung auf bestimmte Spalten

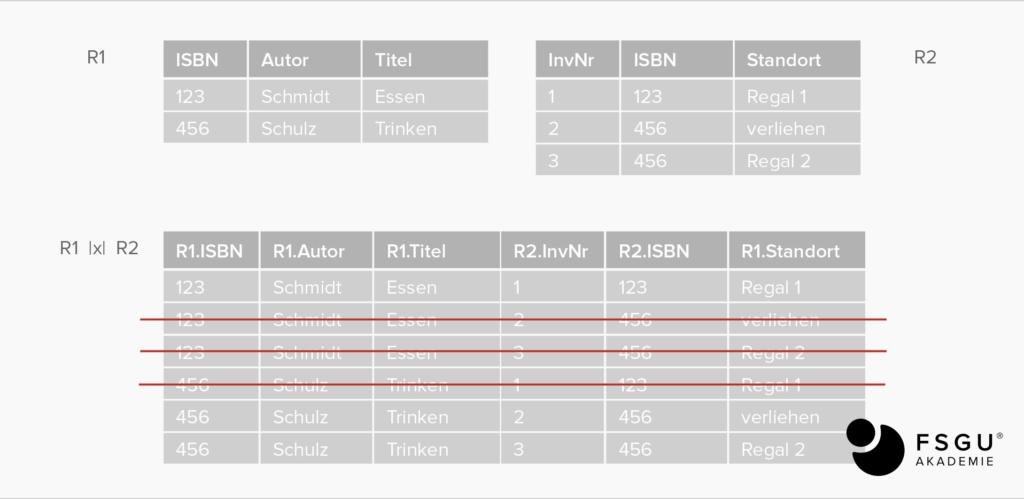
(Natürliche) Verbindung: R1 JOIN R2
alle mögl. Kombinationen der Tupel aus R1 u. R2; „gemeinsame Attribute dienen als Verknüpfung“, Verknüpfung bei gemeinsamen Attributen ist über Fremdschlüssel -> Primärschlüssel gegeben.

Division: R1 DEVIDEBY R2

R1 muss mindestens alle Attribute von R2 enthalten (R2 ist Teilmenge von R1). Die neue Relation

• enthält nur die Attribute, die R1 zusätzlich zu R2 hat
• enthält nur die Tupel von R2 deren Attribute mit denen von R1 übereinstimmen.
• nur die „neuen“ Attribute werden gewählt (d.h. nur in R1 enthalten)
• nur die Tupel werden gewählt, wo für die Attribute gilt, die in R1 und R2 vorhanden sind: „die Attribute stimmen in ihren Werten überein“

Dazu einige Beispiele anhand eines Kreditinstituts nach (Fink, 2003):

An Relationen (Tabellen) sei gegeben

KONTO (Filiale, Kto#, KName, Saldo)
KUNDE (KName, KStraße, KStadt)
KREDIT (Filiale, Kredit#, KName, Betrag)

„Finde alle Kunden aus der Stadt Hamburg“➟ 

Selektion KStadt=Hamburg (KUNDE)

„Finde alle Namen von Kunden aus der Stadt Hamburg“ ➟

Projektion KName (Selektion KStadt=Hamburg (KUNDE))

„Finde alle Kunden, die einen Kredit besitzen, und gebe den Kundennamen, dessen Stadt, sowie die Kreditsumme aus“ ➟

1. Bildung des kartesischen Produkts von KUNDE und KREDIT
2. Selektion solcher Verknüpfungen, bei denen KName übereinstimmt (➟ Join)
3. Projektion der Attribute KName, KStadt und Betrag ➟

Projektion KUNDE.KName, KUNDE.KStadt, KREDIT.Betrag  
(Selektion KUNDE.KName=KREDIT.KName (KUNDE x KREDIT))