Was ist eine Nutzenfunktion?
Eine Nutzenfunktion ordnet jedem Güterbündel X (aus dem Konsumraum) genau eine reelle Zahl, die Nutzenzahl U(X) zu. Dabei ist die Nutzenzahl für zwei Güterbündel gleich, wenn diese als indifferent gesehen werden. Die Nutzenzahl eines Güterbündels X1 ist größer als der des Güterbündels X2, wenn der Haushalt das Güterbündel X1 präferiert:
U(X1) > U(X2) ⇔ X1 ≻ X2
U(X1) < U(X2) ⇔ X1 ≺ X2
U(X1) = U(X2) ⇔ X1 ∼ X2
Wir wollen sogleich bemerken, dass beim Vorliegen einer Nutzenfunktion die Axiome des Rationalverhaltens erfüllt sind!
Zugleich bemerken wir, dass es zu jeder Präferenzordnung verschiedene Nutzenfunktionen geben kann, die diese abbilden. Umgekehrt gehört jedoch jede Nutzenfunktion nur zu genau einer Präferenzordnung.
Wir unterstellen eine Ordinale Nutzenfunktion: Die Präferenzordnung legt nur eine Rangordnung zwischen Güterbündeln fest, sagt jedoch nichts darüber aus, um wieviel ein Gut bzw. Güterbündel gegenüber einem anderen Gut bzw. Güterbündel besser eingeschätzt wird. Wir können also nicht sagen, dass wir eine Banane „doppelt so gerne haben“, auch wenn U(Banane) = 4 und U(Erdbeere)=2.
Wichtig: Setzen Sie „Nutzen“ nicht mehr Geldbeträgen gleich! Der Nutzen ist eine abstrakte Größe und hat unmittelbar nichts mit Geld oder Gütermengen zu tun.
Beispiele für Nutzenfunktionen sind vielfältig und generell kommen alle multivariaten Funktionen in Frage:
Was ist das Grenznutzen des Gutes i?
Der zusätzliche Nutzen, den der Haushalt daraus zieht, dass er eine (marginale) Mengeneinheit des Gutes i mehr verbraucht wird Grenznutzen des Gutes i genannt.
Man schreibt für den Grenznutzen
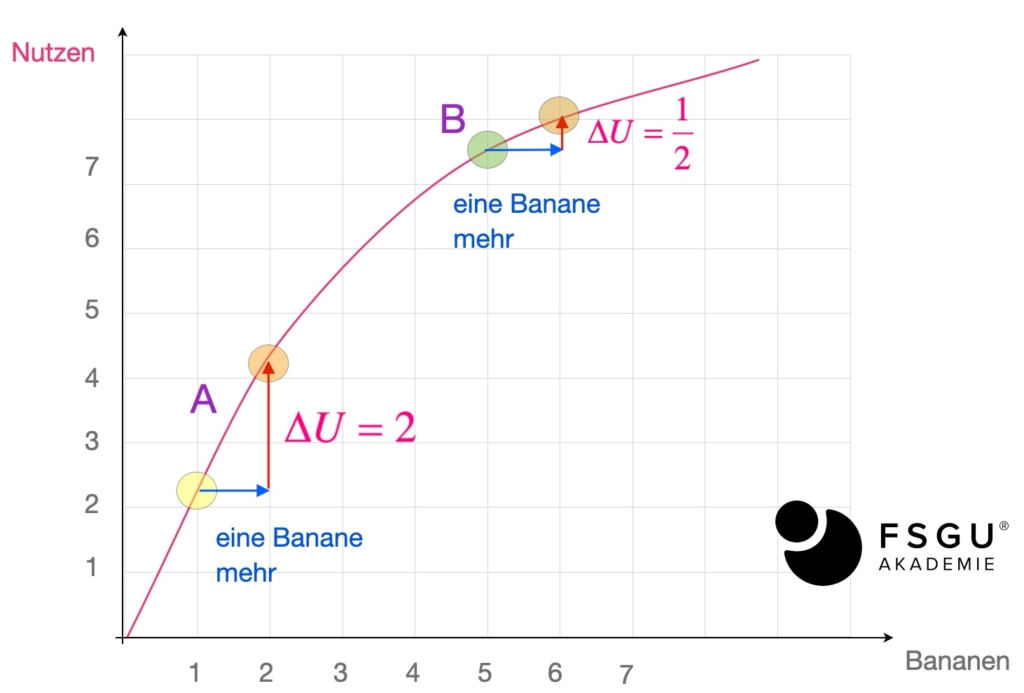
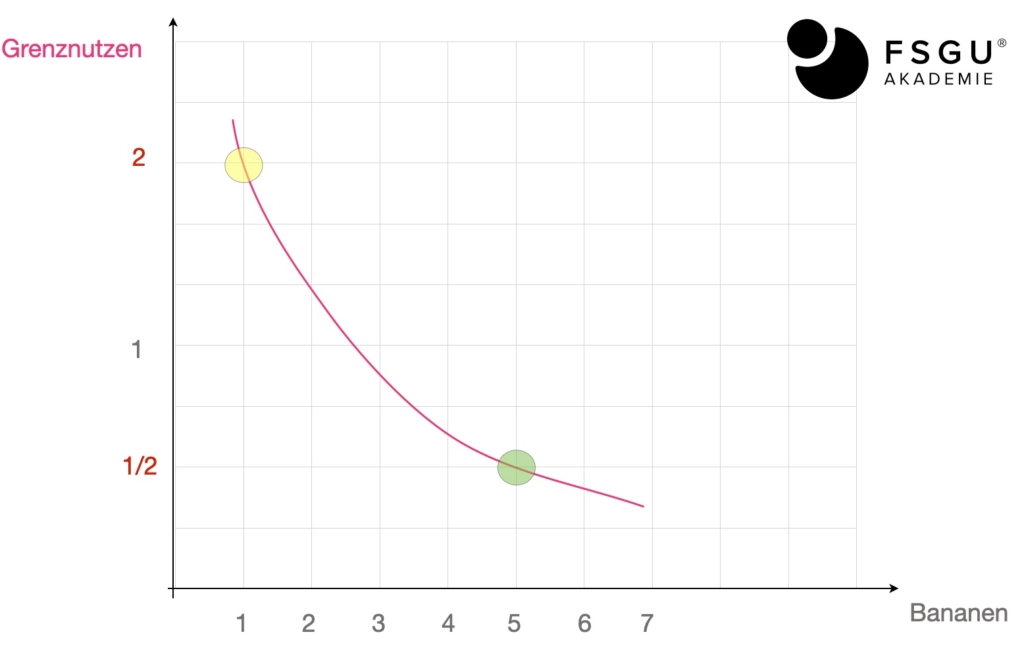
Wir gehen davon aus, dass der Grenznutzen positiv ist, das folgt unmittelbar aus der Annahme der Nichtsättigung. Denn erhöhen wir wie in den unteren Grafiken dargestellt die Bananenzahl von 1 auf 2 (Punkt A), so haben wir einen zusätzlichen Nutzen von ca. 2.
Im Punkt B erhöhen wir die Zahl der Bananen von 5 auf 6. Dabei steigt der Nutzen zwar nicht mehr so stark an (nur noch um 0,5), aber der Grenznutzen ist nach wie vor positiv.
Was ist die Grenzrate der Substitution?
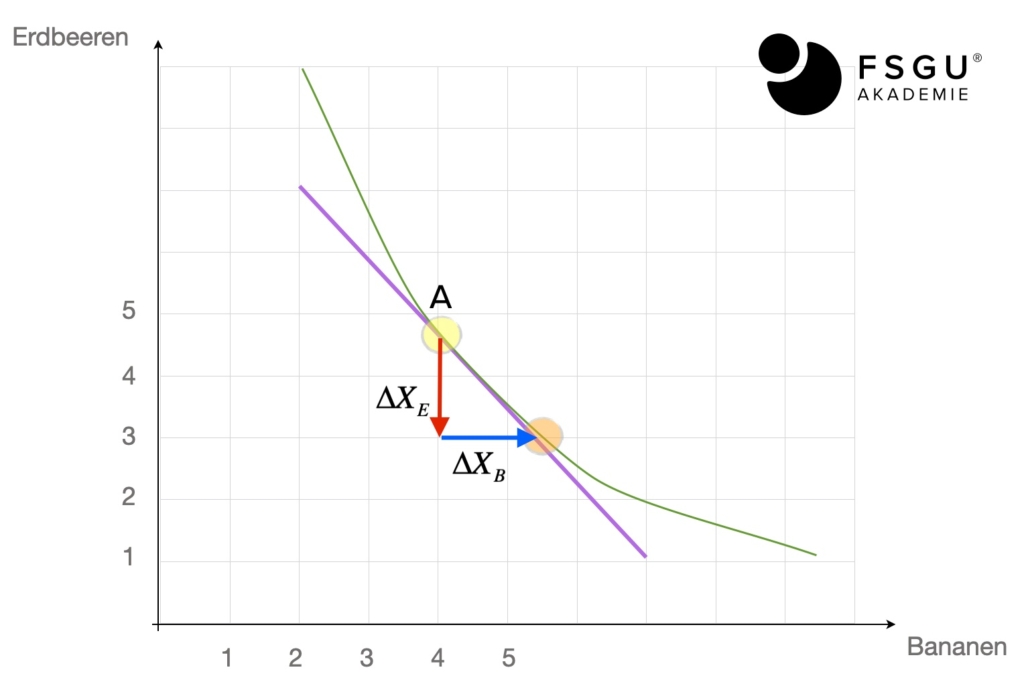
Anhand der obigen Grafik errechnen wir die GRS zu 1,38.
Dabei ist die jeweilige Länge der beiden Pfeile entscheidend, die wir (grob) zu 1,8 und 1,3 entnehmen wollen.
Übrigens hätten man die Pfeile auch umgekehrt darstellen können, daher ist es egal, ob das Minuszeichen im Nenner oder Zähler steht.
Die Grenzrate der Substitution gibt an, auf welche Menge an Erdbeeren ein Haushalt zu verzichten bereit ist, wenn sich die „Bananenmenge“ um eine (marginale, d.h. ganz kleine) Einheit erhöht.
Dabei bleibt der Nutzen gleich! Nach wie vor befinden wir uns auf der gleichen Indifferenzkurve, obwohl durch die Substitution vom gelben in den orangenen Punkt übergegangen wurde.
Mathematisch: Die Grenzrate der Substitution entspricht der Tangentensteigung im gelben Punkt A. Diese Tangentensteigung ist negativ.
Wichtig! Grenzrate der Substitution ist positiv definiert! Daher wird vor den Bruch ein „Minuszeichen“ eingefügt.
Allgemein gilt für den Zusammenhang zwischen Grenzrate der Substitution und den Grenznutzen zweier Güter:
Auf der Indifferenzkurve ändert sich der Nutzen nicht:
Die Grenzrate der Substitution von Gut 2 durch Gut 1 ist gleich dem Verhältnis des Grenznutzen von Gut 1 zum Grenznutzen von Gut 2.
Wegen der Nichtsättigungsannahme sind beide Grenznutzen positiv – dann „muss“ die Grenzrate der Substitution positiv definiert werden, da die Tangentensteigung wegen der fallenden Indifferenzkurve ja negativ ist.
Gesetz von der abnehmenden Grenzrate der Substitution (1.Gossensches Gesetz):
Je mehr ein Haushalt bereits von einem Gut (Bananen) besitzt, desto weniger wird er von einem anderen Gut (Erdbeeren) aufzugeben bereit sein, um noch eine zusätzliche Mengeneinheit des ersten Gutes zu erhalten.
Man kann sagen, das der Zusatznutzen (der Grenznutzen) eines Gutes umso geringer ist, je mehr davon verbraucht wurde.
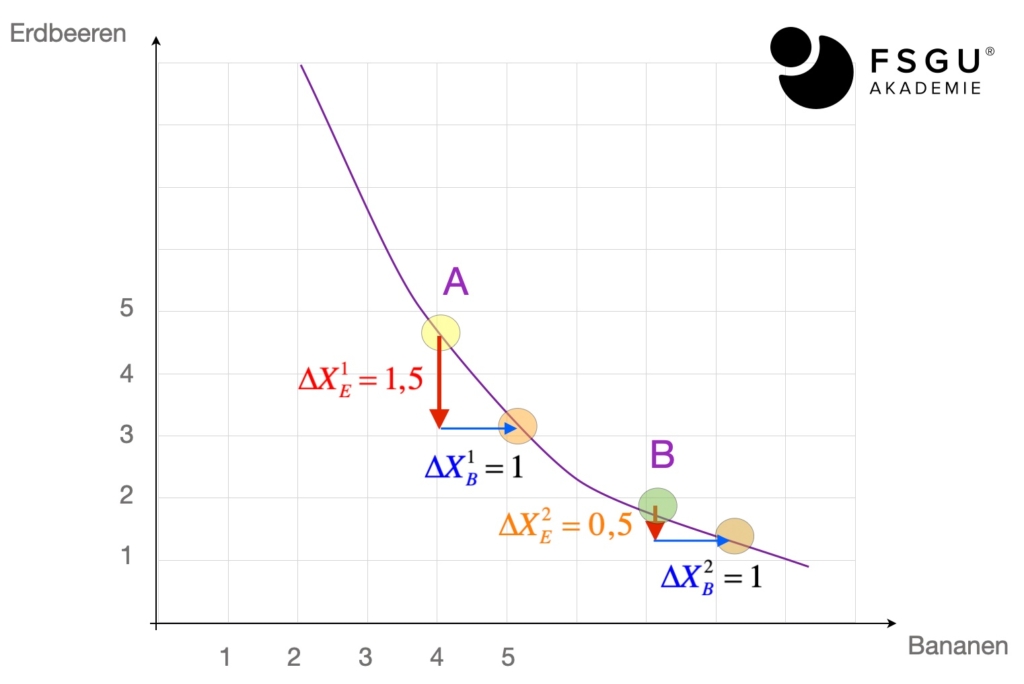
Punkt A: Für (ca.) eine Banane mehr (man schreibt: △XB1=1)
wäre hier der Haushalt bereit, auf ca. 1.5 Erdbeeren zu verzichten (△XE1=1,5), wenn sich das Nutzenniveau nicht ändern soll!
Punkt B: Für (ca.) eine Banane mehr (man schreibt: △XB2=1)
würde der Haushalt hier nur auf ca. 0,5 Erdbeeren verzichten (△XE2=0,5), wenn sich das Nutzenniveau nicht ändern soll!
Als nächstes wollen wir uns verdeutlichen, wieso eine betraglich steigende Grenzrate der Substitution nur bei streng konkaven Indifferenzkurven der Fall sein kann.
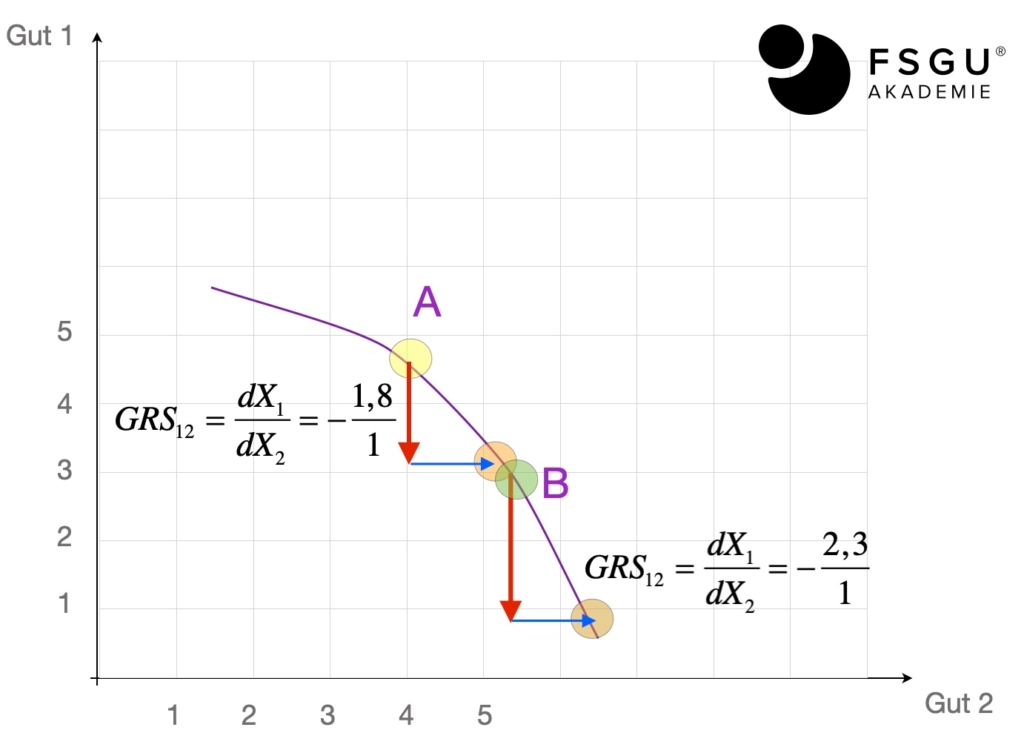
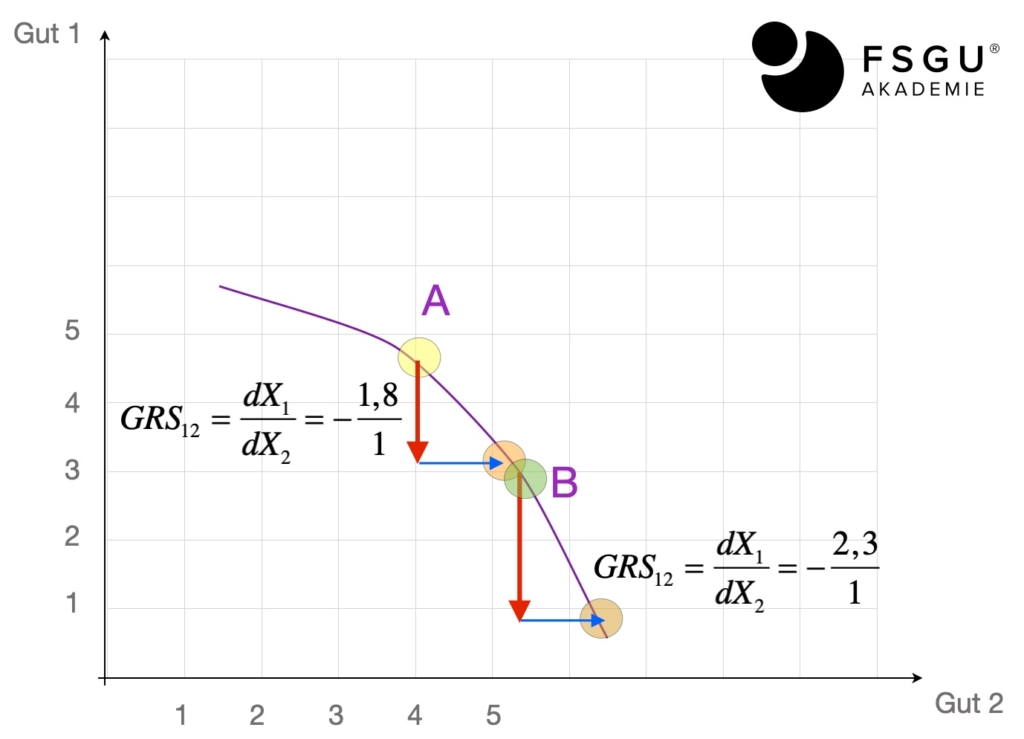
Erhöhen wir sukzessive die Menge des zweiten Gutes (das wir hier an der x-Achse abtragen), so wird die Steigung der Tangente betraglich zunehmen, die Tangenten sind also immer steiler.
Im Beispiel erkennt man dies durch den Übergang von Punkt A in den Punkt B. Während in A die GRS bei (betraglich) 1,8 liegt, ist sie in B schon bei 2,3.
Indifferenzkurven können also sowohl konvex wie auch konkav verlaufen. Auch können sie linear verlaufen, das werden wir gleich noch sehen. Je nachdem verhält sich dann auch die Grenzrate der Substitution.
Fassen wir zusammen:
- Eine betraglich steigende Grenzrate der Substitution haben wir nur bei streng konkaven Indifferenzkurven.
- Eine betraglich fallende Grenzrate der Substitution haben wir nur bei streng konvexen Indifferenzkurven.
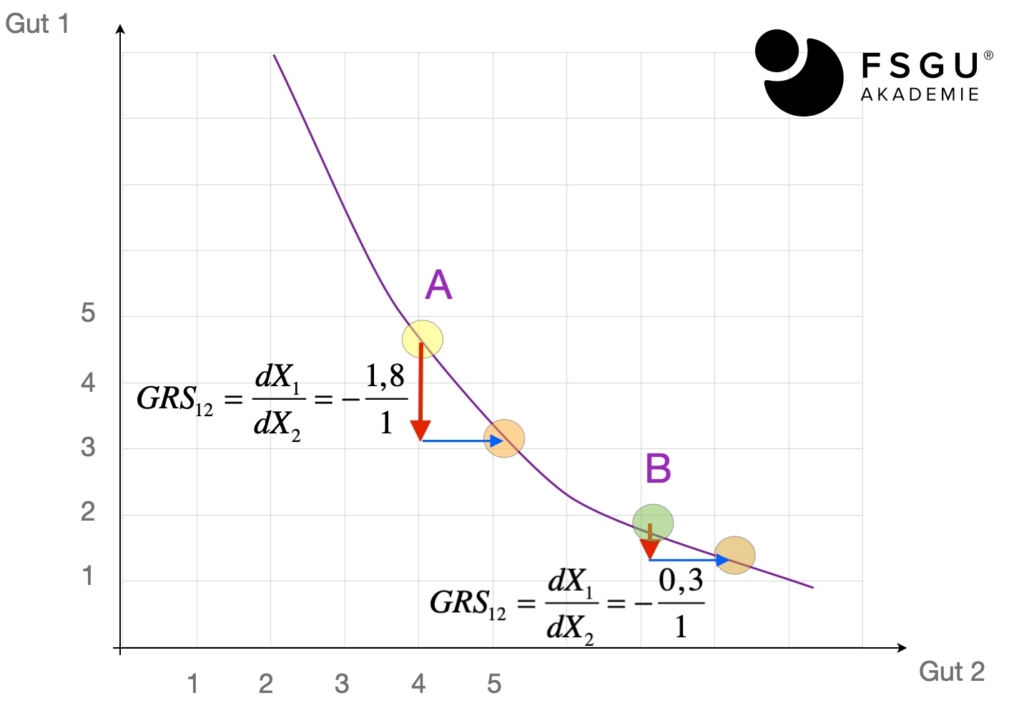
Man bemerke, dass wir hier an der X-Achse das Gut 2 abtragen. Meist werden wir es in Zukunft so handhaben, dass wir dort Gut 1 abtragen. Dann ändert sich entsprechend die GRS dahingehend ab, dass wir den Kehrwert bestimmen müssen.
Wir fragen uns: Wie „leicht“ kann man zwei Güter gegeneinander substituieren?
Zur Wiederholung: Die Preiselastizität der Nachfrage gibt an, um wieviel Prozent die Nachfrage sinkt, wenn der Preis um ein Prozent steigt.
Die Substitutionselastizität gibt an, um wieviel Prozent (bei gleichem Nutzenniveau) das Verhältnis der Gütermengen X2 / X1 steigt, wenn die Grenzrate der Substitution um ein Prozent steigt.
Sie ist Maß für die Krümmung der Indifferenzkurve.
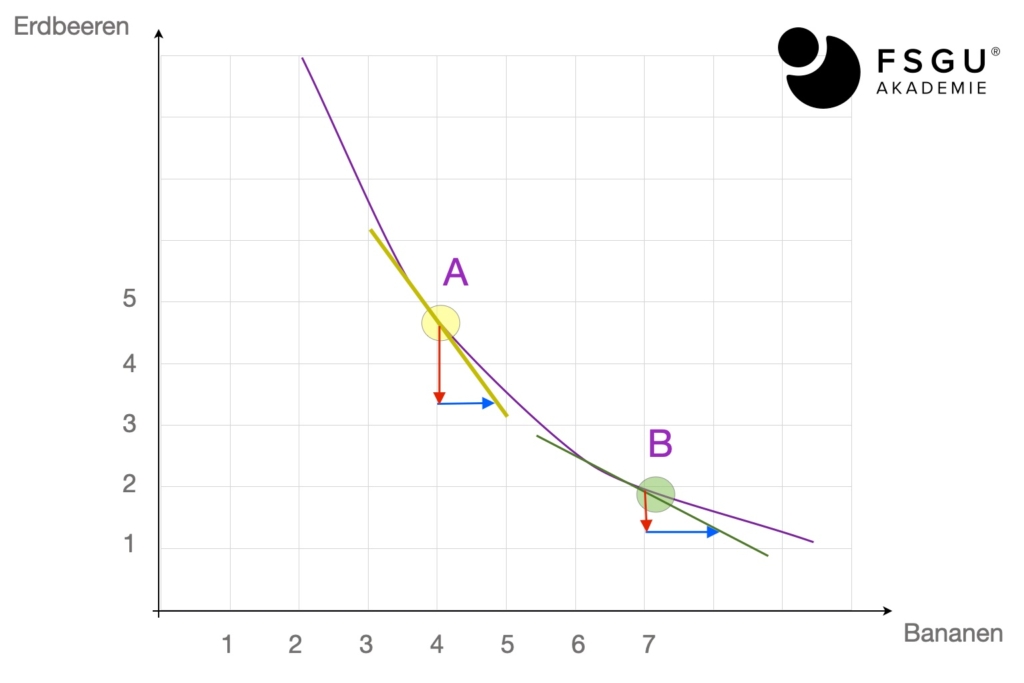
Betrachten wir den Übergang von Punkt A zu Punkt B :
Die GRS(Erdbeeren,Bananen) sinkt (beachte GRS ist positiv definiert) im obigen Bild von etwa 2 zu 1, der rote Pfeil wird also kleiner.
Das Verhältnis Erdbeeren zu Bananen sinkt ebenfalls:
Substitutionselastizität:
Ist die relative Änderung des Güterverhältnisses zur relativen Änderung der Grenzrate der Substitution.
Wenn die GRS(Erdbeeren,Bananen) um ein Prozent sinkt, dann sinkt das Verhältnis Erdbeeren zu Bananen genau um 1,4921 Prozent
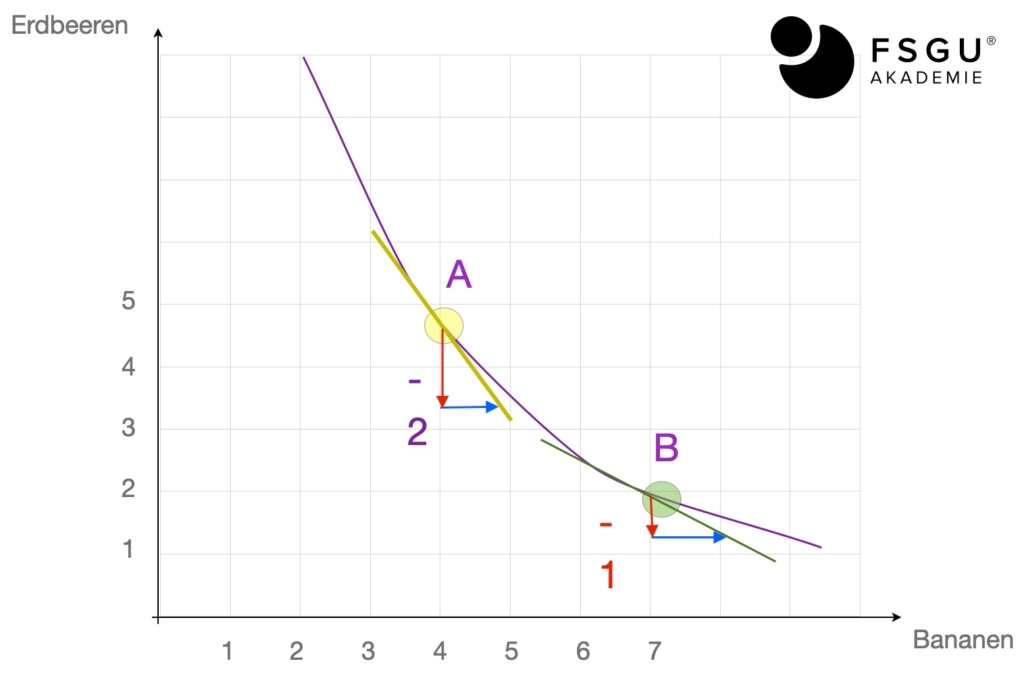
Betrachten wir den Übergang von Punkt A zu Punkt B :
Die GRS(Erdbeeren,Bananen) sinkt (beachte GRS ist positiv definiert) im obigen Bild von etwa 2 zu 1, der rote Pfeil wird also kleiner.
Das Verhältnis Erdbeeren zu Bananen sinkt ebenfalls:
Welche Spezialfälle hat die Substitutionselastizität?
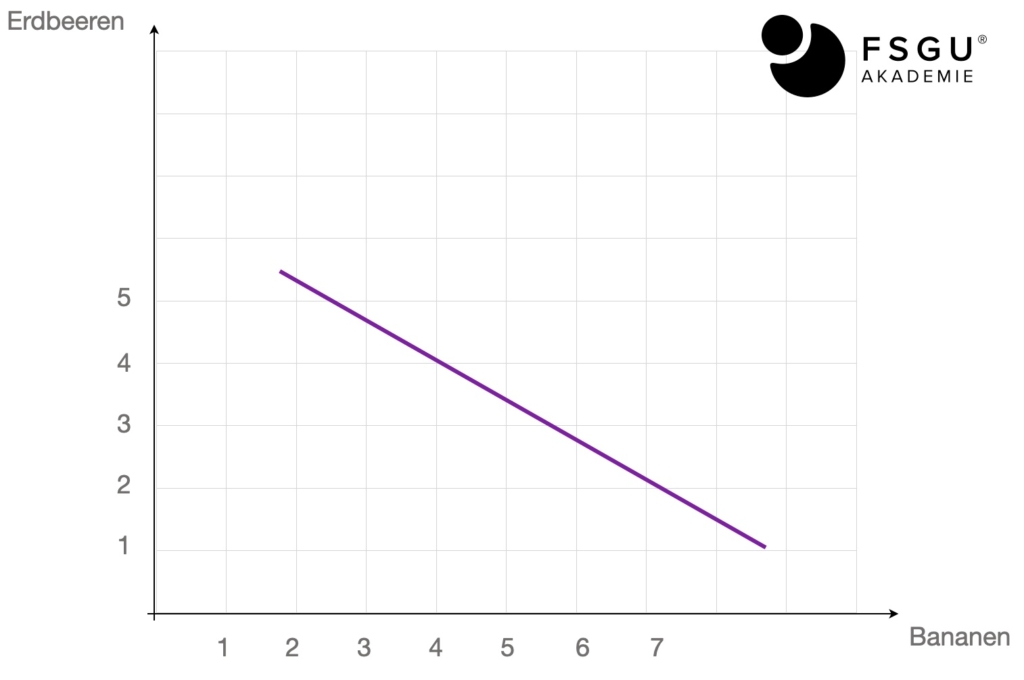
Lineare Indifferenzkurve
Die GRS(E,B) bleibt immer gleich, da die Indifferenzkurve linear ist.
=> keine Veränderung bei GRS (E,B).
=> Nenner der Substitutionselastizität „praktisch“ Null.
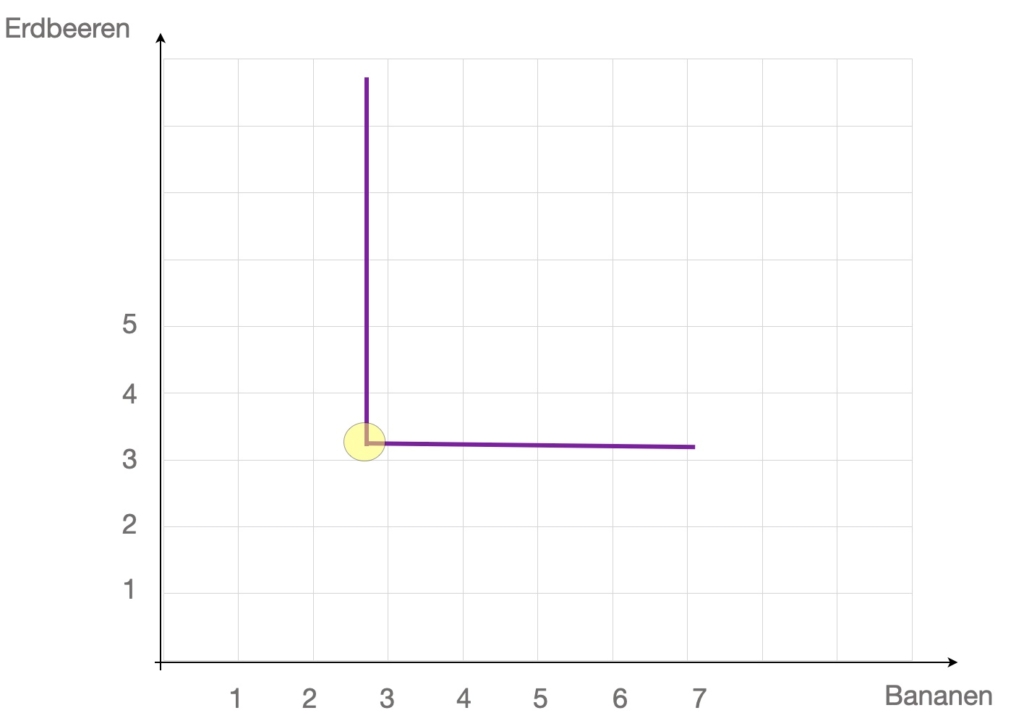
Rechtwinklige Indifferenzkurve (limitational)
Das Güterverhältnis bleibt immer gleich.
=> Der Zähler ist gleich Null.
Je stärker die Kurve gekrümmt ist, umso kleiner ist die Substitutionselastizität.