Was sind die Instrumente der Prozesskontrolle?
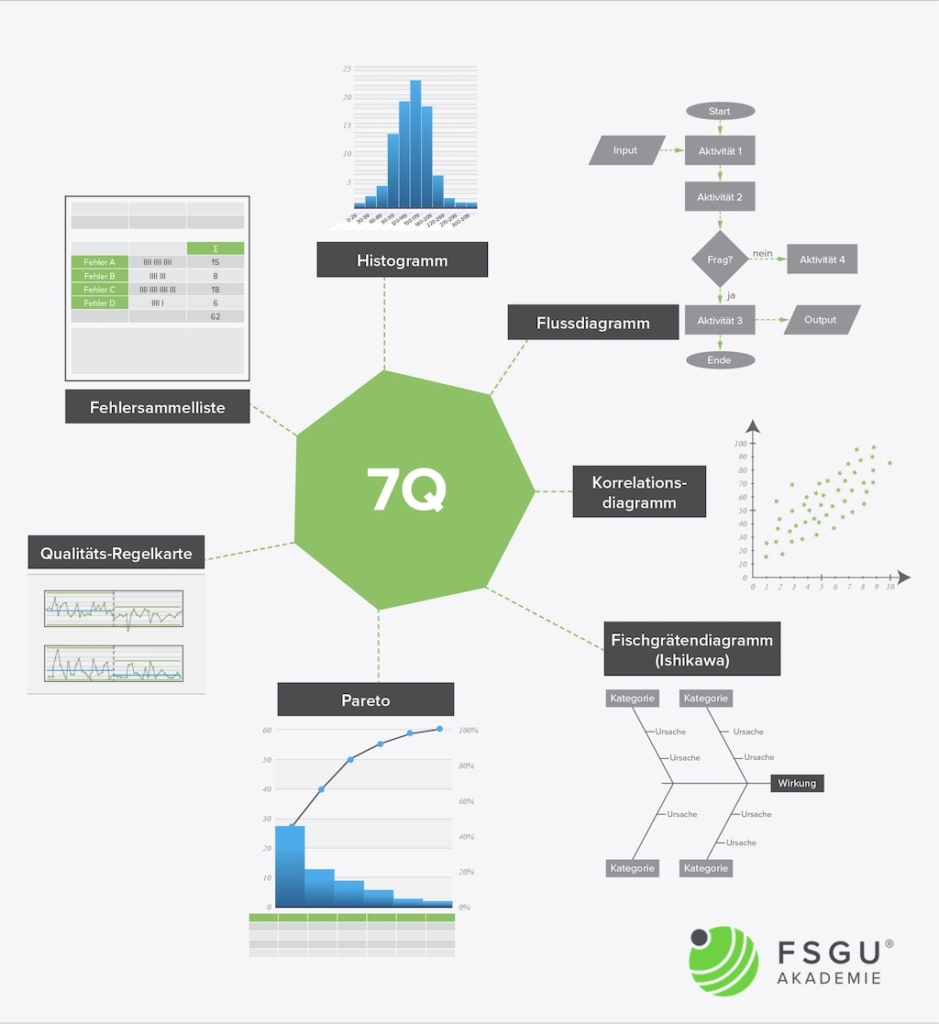
Was sind die Sieben Werkzeuge der Qualität (7Q)?
„7Q“ steht als Synonym für die „Sieben Werkzeuge der Qualität“. Diese wurden in den 40er Jahren des vorigen Jahrhunderts vom japanischen Chemiker Kaoru Ishikawa (1915 – 1989) entwickelt und gelangten ursprünglich in den Qualitätszirkeln seines „Company Wide Quality Control“ (CWQC) Konzeptes zur Anwendung.
Heute sind die sieben Qualitätswerkzeuge in industriellen Unternehmen aller Branchen weitverbreitet und gelten als unverzichtbare Bestandteile kontinuierlicher Verbesserungsprozesse.
Was beinhaltet die Fehlersammelliste?
Eine einfache Art der Erfassung stellt die Fehlersammelliste dar. Sie dient dazu, beobachtete Fehler nach Art und Häufigkeit in einer übersichtlichen Darstellung auszuweisen.
Bevor eine Fehlersammelliste aktiviert werden kann, muss die zu untersuchende Problemstellung eindeutig definiert sein. Nach erfolgter Definition sind die erwarteten Fehlerarten aufzulisten, dabei ist es wichtig, auch eine Kategorie für „nicht klassifizierter Fehler/Sonstiger Fehler“ vorzusehen. Erfasst werden meist die direkte Fehleranzahl, aber auch gewichtete Größen wie die Fehleranzahl multipliziert mit den Fehlerkosten oder die Fehleranzahl multipliziert mit der Bedeutung für den Kunden (kundenorientierte Auswertung).
Des Weiteren ist festzulegen, wer für die Erfassung der Fehler verantwortlich ist und vor allem zu welchen Zeitpunkten, in welchen Intervallen und über welchen Zeitraum mit der Fehlersammelliste gearbeitet wird.
Sind alle oben erwähnten Parameter definiert und festgelegt, kann ein Erfassungsbogen (auch „Erhebungsbogen“) angelegt werden. Die Ausführung und Gestaltung des Erfassungsbogens unterliegt keiner strengen Beschränkung, sondern kann für jeden Anwendungsfall unterschiedlich ausfallen. Es ist in diesem Zusammenhang allerdings empfohlen, den Erfassungsbogen zweckmäßigerweise im Vorfeld durch Nutzung in einem „Testbetrieb“ auf seine Eignung hin zu untersuchen.
| Fehler | Januar | Februar | März | ∑ |
|---|---|---|---|---|
| Verkantet | III | | 24 | |
| Verschleiß | | | | 35 |
| Steuerungsfehler | III | | II | 11 |
| Programmfehler | I | II | | 8 |
| Werkstück lose | | | | 44 |
| Übergabefehler | | III | | 24 |
| Gesamt: | 62 | 41 | 43 | 146 |
Beispiel einer Fehlersammelliste (Quelle: www.was-ist-qm.de)
Obwohl der Aufbau und die Anwendung einer Fehlersammelliste einfachen Kriterien genügt, können sich doch erhebliche Schwierigkeiten und damit fehlerhafte Erfassungen und Auswertungen ergeben.
Vor allem ist sicherzustellen, dass die für die Erfassung von Fehlern beauftragten Personen qualifiziert sind, aufgetretene Fehler eindeutig zu erkennen und einer Fehlerart zuzuordnen. Dies ist besonders dann von Bedeutung, wenn der Erfassungszeitraum mehrere Tage umfasst und somit mehrere unterschiedliche Personen die Eintragungen vornehmen.
Es ist des Weiteren empfehlenswert, aus Gründen der Übersicht den Umfang der zu erfassenden Fehler auf ein akzeptables Maß zu reduzieren, um im Verlauf der Erfassung fehlerhaften Fehlerzuordnungen oder eine durch Zeitmangel bedingte zu häufige Klassifikation „sonstiger Fehler“ zu vermeiden.
Nach Abschluss der Datenerfassung gibt die Fehlersammelliste unmittelbar Aufschluss über die Verteilungshäufigkeit der erfassten Fehler.
Hinweis: Wenn das Fehlermerkmal „nicht klassifizierter Fehler/sonstiger Fehler“ mit der höchsten oder zweithöchsten Anzahl an Fehlern vorliegt, ist das Ergebnis nicht eindeutig, da offensichtlich eine oder mehrere wichtige Fehlerarten nicht definiert wurden. Hier ist eine neuerliche Fehlererfassung mit geänderter Fehlerdefinition zu empfehlen.
Was beinhaltet das Histogramm?
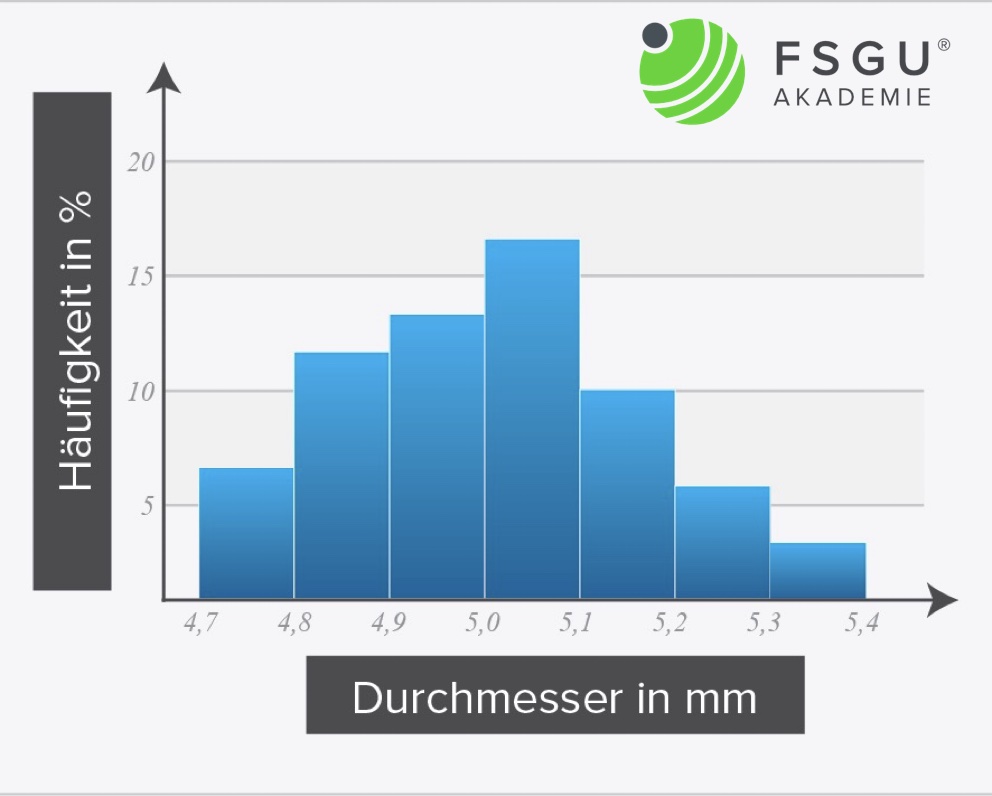
Zur Visualisierung von Häufigkeiten aus einem großen Satz von Daten bedient man sich eines Säulendiagramms – des sogenannten Histogramms.
Damit ist es möglich, tabellarisch vorliegende Informationen „lesbar“ zu machen, zusätzlich ist es mit dem Histogramm möglich, Zielwerte und Toleranzen anzugeben. Mit der Definition dieser Zielwerte und Toleranzen kann für einen durch diverse Daten erfassten Prozess rasch eine Aussage über seine Schwankung („Streuung“) getroffen werden.
Für die Erstellung eines Histogramms sind tabellarische Eingangsdaten notwendig, z.B. die gemessene Länge einer Serie von Bauteilen aus einem Herstellprozess. Um ein aussagekräftiges Histogramm zu erhalten, sind zumindest 50 Einzelmessungen vonnöten.
Die Einzeldaten lassen nun die Berechnung der Spannweite R zu, wenn man den kleinsten gemessenen Wert von dem größten subtrahiert:
Annahme: Wenn man die Länge eines Bauteiles mit einem Sollmaß von 100mm mit einem präzisen Messmittel auf 1/100mm genau misst, wird man kaum übereinstimmende Einzelmaße erhalten. Es ist daher sinnvoll, näherungsweise Klassen K nach folgender Formel zu bilden:
Diese Näherung kann bei Werten von K zwischen fünf und 25 angewendet werden. Ist K < 5, wird das spätere Histogramm aufgrund der geringen Anzahl an Klassen wenig Aussagekraft besitzen, andererseits ist mit K > 25 im Histogramm keine Übersichtlichkeit mehr gegeben. Nach Bedarf ist also der K-Wert anzuheben oder zu reduzieren.
Die Klassenbreite H errechnet sich danach wie folgt:
Der kleinste Einzelwert stellt die untere Grenze der ersten Klasse dar. Durch Addition der Klassenbreiten werden auf der Abszisse alle Werte der entsprechenden Klasse zugeordnet sowie auf der Ordinate die absolute oder relative (d.h. prozentuale) Klassenhäufigkeit aufgetragen.
Was beinhaltet das Paretodiagramm?
Mit dem Paretodiagramm ist es möglich, Ursachen von Prozessproblemen grafisch in Form eines Säulendiagramms hinsichtlich ihrer Bedeutung darzustellen. Es dient deshalb als wesentliches Instrument bei der Entscheidungsfindung, welche Fehlerursachen in welcher Reihenfolge analysiert und abgestellt werden müssen.
Entsprechend dem Pareto Prinzip ist in den meisten Fällen davon auszugehen, dass 80% der Auswirkungen auf 20% der erfassten Ursachen und Einflussgrößen zurückführbar sind.
Die Datenbasis für das Paretodiagramm bildet meist eine Fehlersammelliste; vergleiche mit dem vorigen Abschnitt.
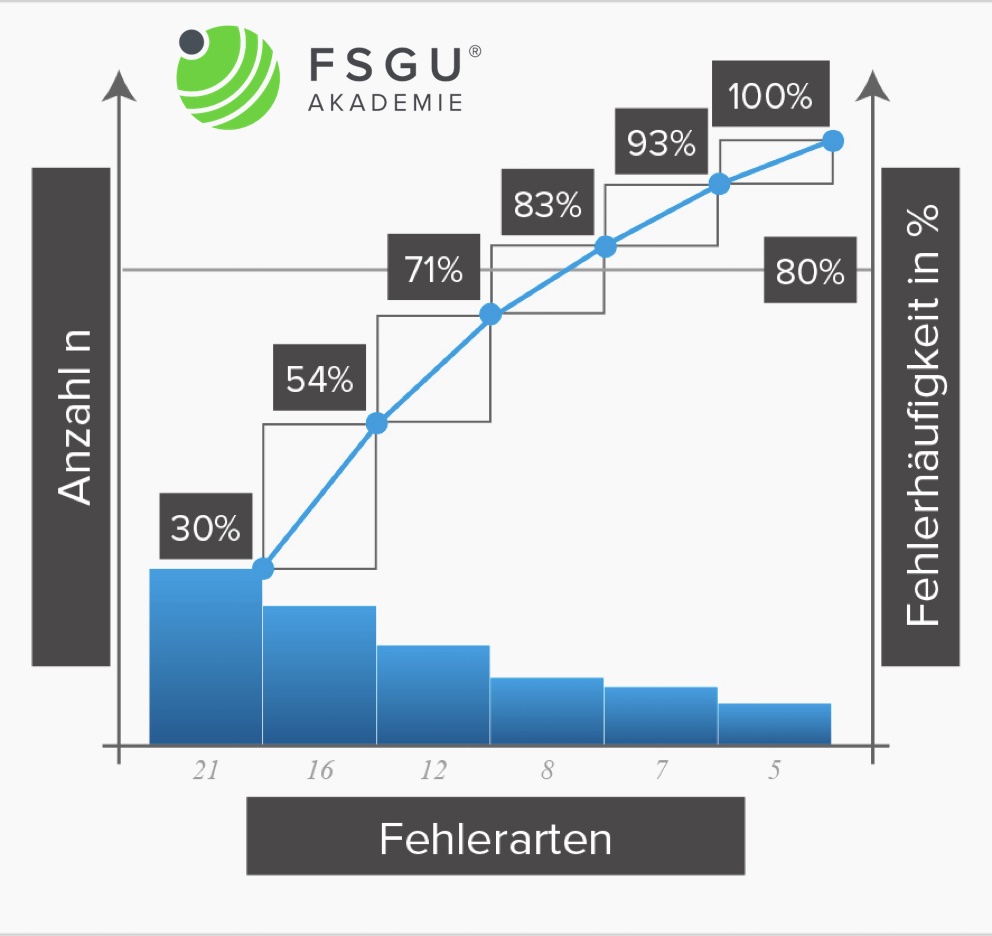
Damit das Diagramm erstellt werden kann, sind die vorliegenden Daten – die absoluten Häufigkeiten der einzelnen Fehlerklassen – in prozentuale Anteile umzurechnen. Danach werden die einzelnen Fehlerklassen entsprechend der vorliegenden prozentuellen Häufigkeit auf der Abszisse aufgetragen, beginnend mit der höchsten Fehlerhäufigkeit.
Üblicherweise enthält das Paretodiagramm zwei Ordinaten. Während die linke Ordinate den prozentualen Anteil der einzelnen Fehlerarten aufträgt, zeigt die rechte Ordinate die kumulierte prozentuelle Fehlerhäufigkeitskurve. Diese kumulierte Kurve beginnt mit 0% bei der ersten Fehlerklasse und schließt mit 100% bei der letzten Klasse ab.
Hinweis:
Wenn die Datenbasis einen hohen Prozentwert des Fehlermerkmals „nicht klassifizierter Fehler/sonstiger Fehler“ ergibt, liefert das Paretodiagramm keine eindeutige Entscheidungshilfe zur Priorisierung der Fehlerursachenbekämpfung. Hier ist eine neuerliche Fehlererfassung mit geänderter Fehlerdefinition durchzuführen.
Zur Entscheidungsfindung, welche Fehlerarten zuerst analysiert und abgestellt werden müssen, ist statt der Fehleranzahl eine verknüpfte Betrachtung von Fehleranzahl und der Bedeutung für den Kunden vorzuziehen.
Was beinhaltet das Korrelationsdiagramm?
Das Korrelationsdiagramm zeigt grafisch die Beziehung zwischen erfassten Wertepaaren auf. Das Muster des Korrelationsdiagramms lässt darüber hinaus Rückschlüsse auf einen statistischen Zusammenhang unterschiedlicher Güte zu.
Wie bei den vorangegangenen Qualitätswerkzeugen sind zuerst Überlegungen anzustellen, welche Wertepaare in die Datenerfassung aufzunehmen sind, um sie einer späteren Untersuchung zuzuführen. Methoden wie z.B. Brainstorming gepaart mit der strukturierten Erfassung von Erfahrungswerten durch Fragebögen können hier zur Entscheidungsfindung eingesetzt werden. Für eine abgesicherte Aussage aus dem Korrelationsdiagramm ist darüber hinaus eine ausreichende Anzahl an Wertepaaren notwendig.
Das Korrelationsdiagramm selbst wird durch Auftragen in das x/y-Koordinatensystem erstellt. Die daraus erhaltene Punktwolke wird in einer linearen Regressionsgeraden der Form
abgebildet und zusammengefasst. Steigt die Regressionsgerade, spricht man von einer positiven Korrelation (k>0), sonst von einer negativen Korrelation (k<0, fallende Regressionsgerade).
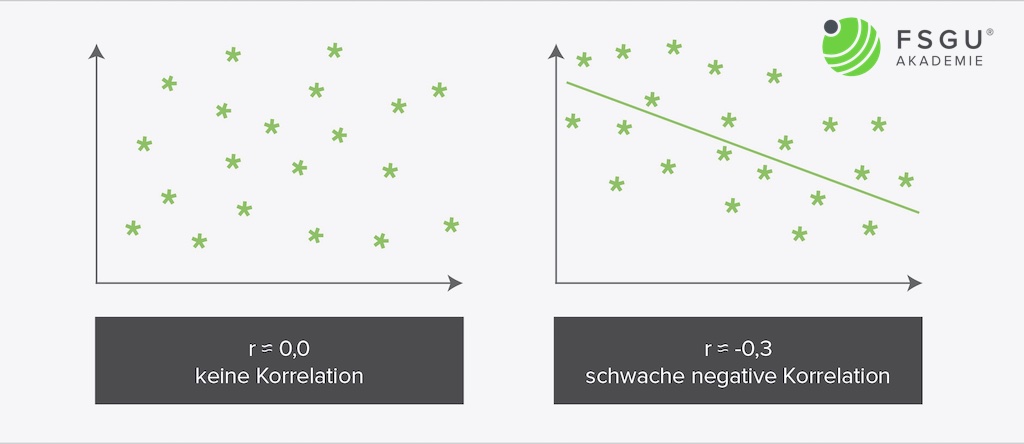
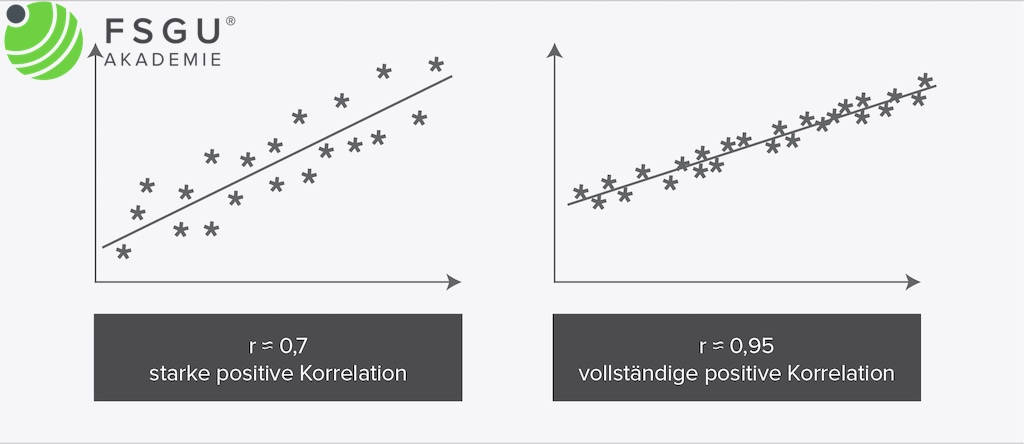
Je näher die einzelnen Werte an der Regressionsgeraden liegen, desto höher ist ihre Korrelation. Als mathematische Maßzahl wird der sog. Korrelationskoeffizient angegeben.
Nachfolgend sei der Korrelationskoeffizient nach Pearson beschrieben:
Der Korrelationskoeffizient ist eine dimensionslose Kennzahl und kann Werte zwischen +1 und -1 annehmen. Das Vorzeichen steht für eine steigende oder fallende Korrelation und die Höhe des Wertes für die Korrelationsstärke. Bei einem Korrelationskoeffizienten von 0 besteht kein Zusammenhang zwischen den Wertepaaren, bei einem Wert von 1 liegen alle Punkte auf der Regressionsgeraden.
Was beinhaltet das Ursachen-Wirkungs-Diagramm?
Das Ursachen-Wirkungs-Diagramm wird häufig auch als Fischgrätendiagramm bzw. nach seinem Erfinder Kaouru Ishikawa als Ishikawa Diagramm bezeichnet.
Das Fischgrätendiagramm ist eine strukturierte Technik der Ursachen- und Problemanalyse. Eine graphische Darstellung stellt die Einflüsse (Ursachen), aufgeteilt in Haupt- und Nebenaspekte, dem Fehler (Wirkung, Auswirkung) gegenüber.
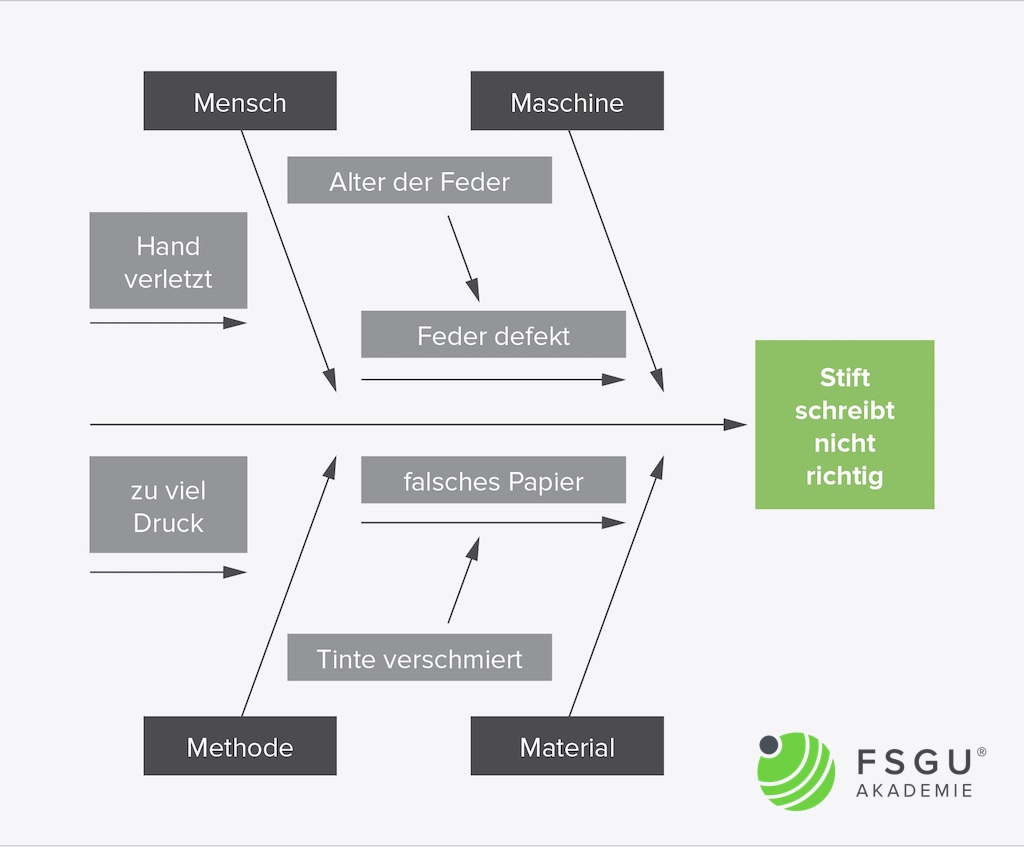
Bevor man mit dem Füllen eines Fischgrätendiagramms beginnt, muss die Problemstellung exakt beschrieben sein. Jede inhaltliche Information, aber auch örtliche, zeitliche oder andere Zusammenhänge mit dem Problem, sind hier von Belang, um einem Problemlösungsteam ein möglichst umfangreiches Bild zu vermitteln. Diese Beschreibung der Problemstellung füllt den rechten Teil des Fischgrätendiagramms (Auswirkung).
Danach ist es notwendig, Kategorien für mögliche Fehlerursachen zu bilden. Je nach Art und Form der Problemstellung bedient man sich verschiedenen Lösungsansätzen, z.B. der 5- M- Methode. Diese Methode klassifiziert in fünf Ursachenkategorien, nämlich „Mensch“, „Material“, „Maschine“, „Methode“ und „Mitwelt“. Diese bilden den linken Teil des Fischgrätendiagramms.
Im eigentlichen Umsetzungsteil der Arbeit mit dem Fischgrätendiagramm gilt es für die Mitglieder des Problemlösungsteams, alle denkbaren Ursachen unter Zuhilfenahme von Kreativitätstechniken wie z.B. Brainstorming zu beschreiben. Die Ursachen werden einer der zuvor definierten Kategorien zugeordnet; graphisch erfolgt dies in Form von Pfeilen, welche auf die jeweiligen Kategorien zeigen.
Die Arbeit mit einem Fischgrätendiagramm bringt durch die intensive Beschäftigung mit und dem Hinterfragen der bekannten möglichen Ursachen oft weitere potentielle Ursachen zum Vorschein.
Nach Abschluss der Ursachenfindungsphase werden die einzelnen Ursachen hinsichtlich ihres Einflusses auf das Problem gewichtet, um daraus eine Prioritätsliste zur Abstellung des Problems zu erhalten.
Hinweis:
Beim Einsatz des Fischgrätendiagramms muss darauf geachtet werden, dass die Ursachen – Wirkungsbeschreibung zu einer vernünftigen Anzahl an Verzweigungsgraden führt. Ist das Fischgrätendiagramm kaum verzweigt, ist diese Methode zur Problemanalyse nicht geeignet. Das Gleiche gilt für hohe Verzweigungsgrade, da hier eine eindeutige Interpretation kaum noch möglich ist. Abhilfe kann in diesem Fall das Splitten der ursprünglichen Problemstellung in mehrere Teilprobleme schaffen.
Was beinhaltet das Ablaufdiagramm?
Mit Hilfe von Ablaufdiagrammen werden Prozesse und deren Wechselwirkungen graphisch und übersichtlich dargestellt. Die Verwendung von standardisierten Symboliken eröffnet Ablaufdiagrammen weite Einsatzgebiete, u.a. auch für Schulungen oder für die Beschreibung von Abläufen im Rahmen eines Qualitätsmanagements.
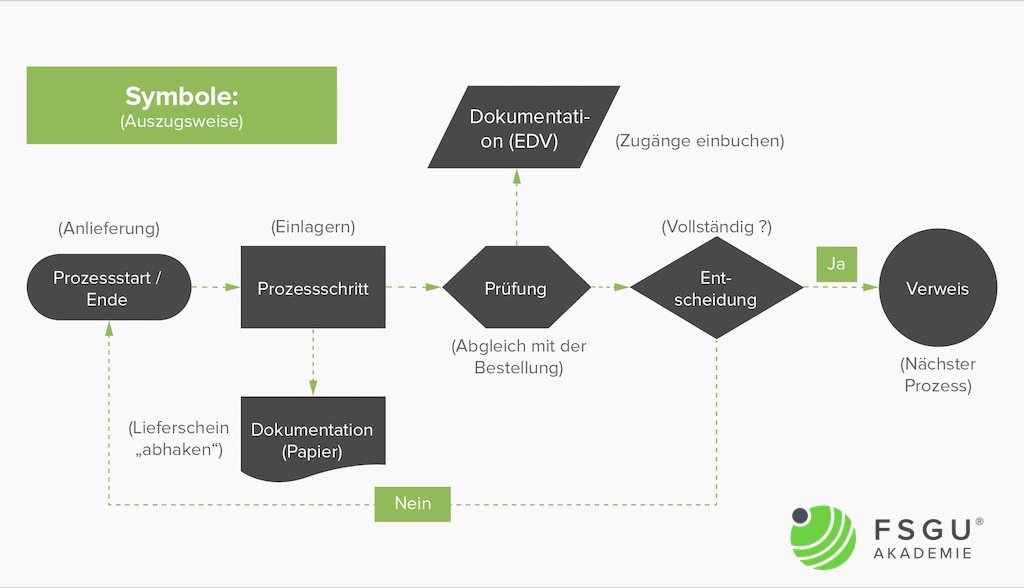
Bei der Erstellung eines Ablaufdiagramms ist es notwendig, den darzustellenden Prozess detailliert in seine einzelnen Schritte zu zerlegen. Informationen über die einzelnen Prozessschritte werden durch Beobachtung oder durch Befragung betroffener Personen durchgeführt. Von besonderem Interesse sind dabei die einzelnen Abhängigkeiten und Wechselwirkungen sowie die dazu existierenden Informationsflüsse, weshalb in dieser Erfassungsphase auf eine ausführliche Dokumentation zu achten ist.
Bereits während der detaillierten Erfassung eines Prozesses für ein Ablaufdiagramm kommen nicht eindeutig geregelte Schritte oder auch Schnittstellenproblematiken hinsichtlich Entscheidungs- oder Durchführungsverantwortungen zum Vorschein und eröffnen Möglichkeiten, an verschiedenen Problemlösungen zu arbeiten.
Die anschließende Visualisierung – die eigentliche Erstellung des Ablaufdiagramms – wird unter Zuhilfenahme von standardisierten Elementen aus der DIN 66001 realisiert.
Was beinhaltet die Qualitätsregelkarte?
Die Qualitätsregelkarte (QRK) oder kurz Regelkarte wird im Qualitätsmanagement zur Auswertung von Prüfdaten eingesetzt.
Das Ziel ist die Bewertung von Prozessen hinsichtlich ihrer zeitlichen Qualitätskonstanz (Prozessstabilität). Wenn sich der Prozess signifikant ändert, wird durch die Qualitätsregelkarte signalisiert, in welche Richtung die Veränderung stattfindet (Vergrößerung der Qualitätsstreuung und/oder Änderung der Lage des Qualitätsmerkmals).
Dazu werden statistische Stichprobenkennwerte (z. B. Stichprobenmittelwert und Stichprobenstandardabweichung des Qualitätsmerkmals) und Warn-, Eingriffs- und Toleranzgrenzen grafisch dargestellt.
Die Prozessregelkarte ist eine Regelkarte, die nicht von vorgegebenen Grenzwerten ausgeht. Die obere und untere Warngrenze sowie die obere und untere Eingriffsgrenze werden aus den vorhandenen Prozessdaten berechnet; sie spiegeln nicht den Toleranzbereich wider, sondern nur die beobachtete Häufigkeitsverteilung der mit dem jeweiligen Schaubild überwachten StichprobenkenngrößeDie Warn- und Eingriffsgrenzen werden periodisch basierend auf den jüngsten Prozessdaten neu berechnet. Die auf Prozessregelkarten gesammelten Prozessdaten bilden die Grundlage für die Prozessfähigkeitsuntersuchung, in der die Häufigkeitsverteilung des beobachteten Merkmals mit dem Toleranzbereich verglichen wird.