Was sind Verteilungsfunktionen?

Was ist die grundsätzliche Klassifizierung?

Verteilungsfunktionen sind mathematische Funktionen, welche eine Auftretenswahrscheinlichkeit bestimmter Merkmalswerte beschreiben. In Abhängigkeit von den Merkmalsausprägungen (attributiv oder variabel) und der jeweiligen Prüfart kommen unterschiedliche Verteilungsfunktionen zur Anwendung.

Verteilungsfunktionen für attributive Merkmale geben dabei an, mit welcher Wahrscheinlichkeit die einzelnen Merkmalswerte auftreten können. In Summe ist die Wahrscheinlichkeit, dass ein Merkmalswert auftritt, logischerweise 1.

Verteilungsfunktionen für variable Merkmale geben hingegen die Wahrscheinlichkeit an, mit der ein reeller Zahlenwert (der Messwert, z.B. Länge, Gewicht) kleiner oder gleich dem Merkmalswert auftritt.

Die untenstehende Abbildung zeigt einen allgemeinen Überblick über die gängigen Verteilungsfunktionen:

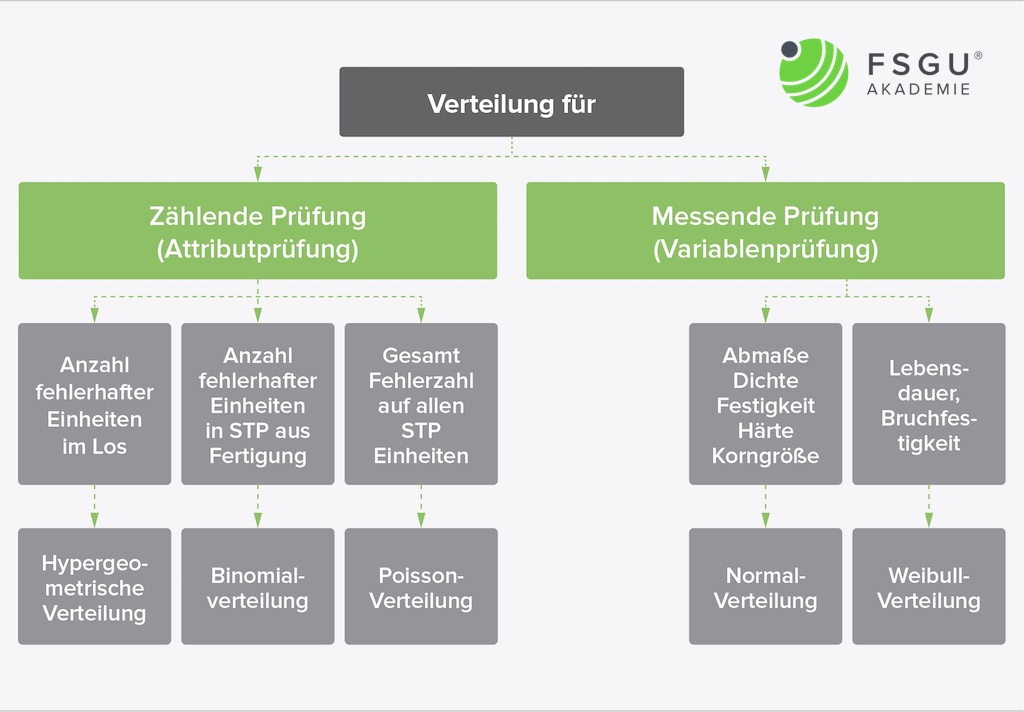
Was ist die hypergeometrische Verteilung?

Die hypergeometrische Verteilung gilt für attributive Merkmale und ist eine Verteilung für klassische „Gut–Schlecht“-Entscheidungen. Anwendung findet die hypergeometrische Verteilung bei Prüfungen, bei denen Stichproben aus dem Prüflos entnommen und nach der Bewertung nicht mehr in den Stichprobenumfang zurückgelegt werden. In der unternehmerischen Praxis wird die hypergeometrische Verteilung dann eingesetzt, wenn das Prüflos kleiner als das 15-20fache des Stichprobenumfangs ist, bzw. in anderen Worten der Stichprobenumfang weniger als 5-6% des Prüfloses ausmacht.

Die Wahrscheinlichkeitsfunktion der hypergeometrischen Verteilung ist mathematisch wie folgt beschrieben:

N….. Größe des Prüfloses 
M….. Anzahl Teile mit Merkmalseigenschaft (z.B. „n.i.O“)
n…… Größe des Stichprobenumfangs
x…… Fehleranzahl im Stichprobenumfang

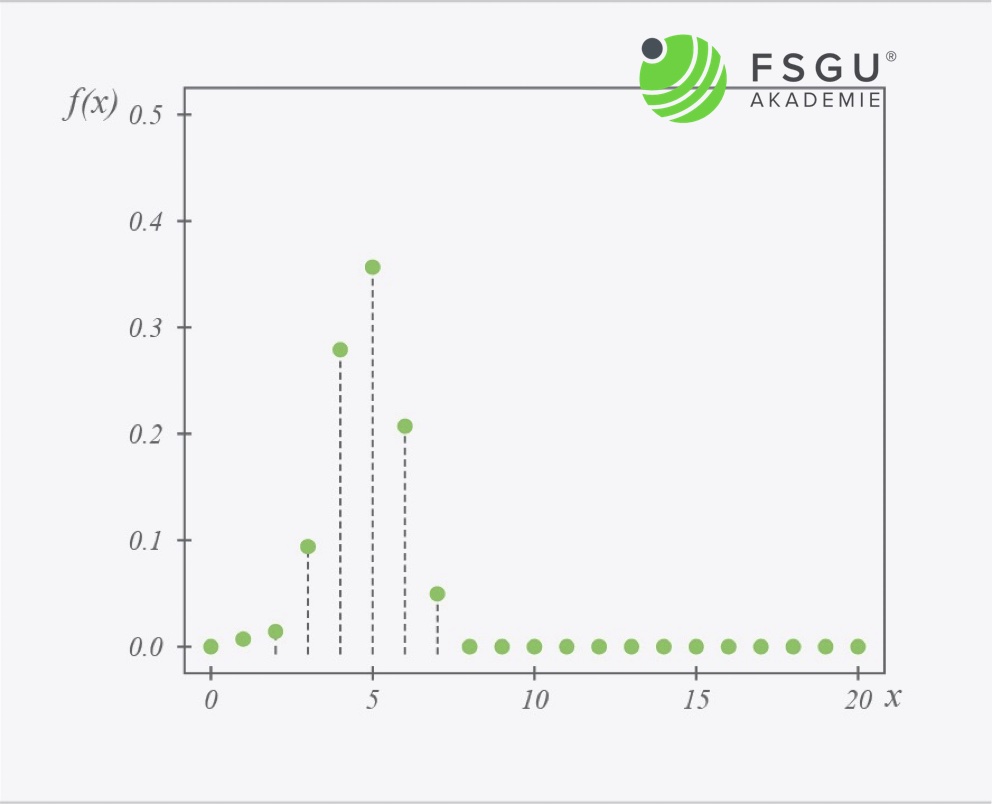
So sieht ein Beispiel für die hypergeometrische Verteilung aus

Ein Prüflos umfasst insgesamt 20 Teile, davon besitzen 12 Teile die Eigenschaft „n.i.O.“. Der Stichprobenumfang beträgt 8 Teile. Die hypergeometrische Wahrscheinlichkeitsfunktion zeigt mit einer Wahrscheinlichkeit von ca. 35%, dass sich 5 n.i.O. Teile innerhalb des Stichprobenumfangs befinden

In diesem Fall ist n=8, N=20, M=12 und x=5. Beachten wir noch, dass gilt:

und weiterhin:

dann erhalten wir insgesamt etwa 35,21%:

Was ist die Binomialverteilung?

Die Binomialverteilung gilt für attributive Merkmale und ist wie die hypergeometrische Funktion eine Verteilung für klassische „Gut-Schlecht“-Entscheidungen.

Anwendung findet die Binomialverteilung bei Prüfungen, bei denen Stichproben aus dem Prüflos entnommen und nach der Bewertung wieder in den Stichprobenumfang zurückgelegt werden. Das Auftreten der Merkmalseigenschaft „n.i.O.“ ist somit bei jeder Einzelentnahme des Stichprobenumfangs gleich wahrscheinlich.

In der unternehmerischen Praxis wird die Binomialverteilung analog zur hypergeometrischen Verteilung dann eingesetzt, wenn der Stichprobenumfang weniger als 5 % des Prüfloses ausmacht.

Die Wahrscheinlichkeitsfunktion der Binomialverteilung ist mathematisch wie folgt beschrieben:

Dabei steht B für die Wahrscheinlichkeitsfunktion und ist so zu verstehen, dass bei n Versuchen genau k Erfolge (i.O.) mit der Wahrscheinlichkeit p^k eintreten. Entsprechend gibt es n-k Fehlschläge (n.i.O.), deren Wahrscheinlichkeit bei (1-p) ^n-k liegt.

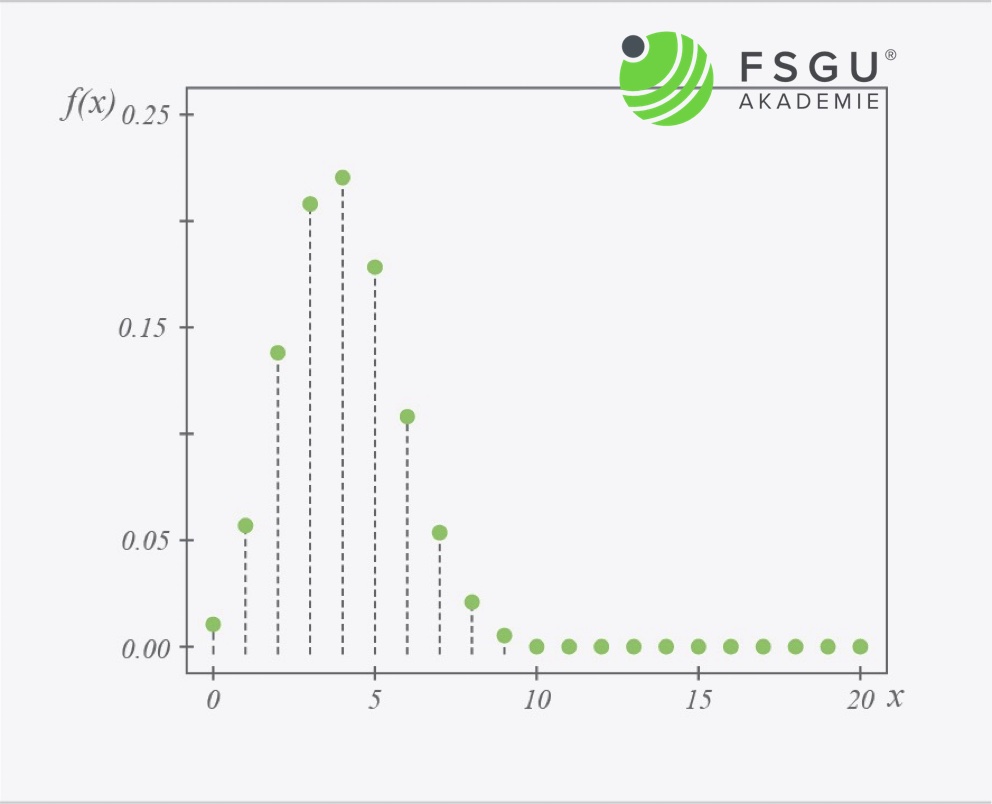
So sieht ein Beispiel für die Binomialverteilung aus

Bei genügend großem Prüflos und einem n.i.O. Anteil (p) von 20% erhält man mit der Binomialverteilung die folgende Wahrscheinlichkeitsfunktion.

Was ist die Poisson Verteilung?

Die Poisson Verteilung findet überall dort Anwendung, wo eine Verteilung für das Auftreten von unerwarteten und vor allem seltenen Merkmalseigenschaften gesucht wird.

Die Wahrscheinlichkeitsfunktion der Poisson Verteilung ist mathematisch wie folgt beschrieben:

λ….. Anzahl Teile mit Merkmalseigenschaft (z.B. „n.i.O“)
x…… Fehleranzahl im Stichprobenumfang

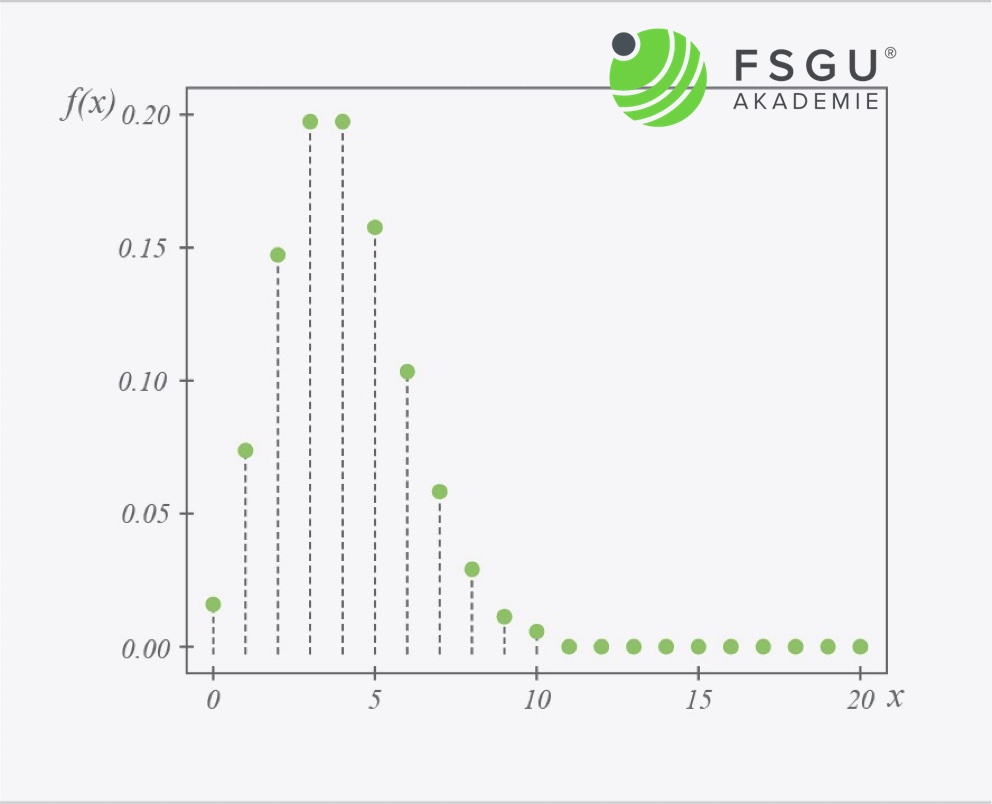
So sieht ein Beispiel für die Poisson Verteilung aus

Innerhalb eines Beobachtungszeitraums von jeweils 20 Tagen wird mit einem Ausfall nach bereits vier Tagen gerechnet. Die Wahrscheinlichkeitsfunktion entsprechend der Poisson Verteilung zeigt die unten abgebildete Form.

Was ist die Normalverteilung?

Die Normalverteilung ist die bekannteste und am häufigsten verwendete Verteilungsfunktion. Kennzeichen der Normalverteilung ist ihre glockenförmige Symmetrie um den Mittelwert herum.

Die Normalverteilung hat in der Qualitätssicherung insofern große Bedeutung, als sie einen klaren Hinweis auf stabile Prozesse gibt. Dies ist im sogenannten zentralen Grenzwertsatz der Statistik begründet, der die Normalverteilung eines Mittelwertes eines Stichprobenumfangs postuliert, wenn:

• die Messwerte innerhalb der Stichprobe voneinander unabhängig sind
• das Prüflos bzw. der dazugehörige Prozess Stabilität zeigt

Die Wahrscheinlichkeitsfunktion der Normalverteilung ist mathematisch wie folgt beschrieben: 

μ steht dabei für den arithmetischer Mittelwert und σ für die Standardabweichung. Diese beschreibt die Breite der Normalverteilung.

Zufallsvariablen mit Normalverteilung benutzt man zur Beschreibung zufälliger Vorgänge wie: 

• zufällige Messfehler,
• zufällige Abweichungen vom Sollmaß bei der Fertigung von Werkstücken,
• Beschreibung der brownschen Molekularbewegung.

In der Versicherungsmathematik ist die Normalverteilung geeignet zur Modellierung von Schadensdaten im Bereich mittlerer Schadenshöhen. 

In der Messtechnik wird häufig eine Normalverteilung angesetzt, die die Streuung der Messfehler beschreibt. Hierbei ist von Bedeutung, wie viele Messpunkte innerhalb einer gewissen Streubreite liegen. 

Viele der statistischen Fragestellungen, in denen die Normalverteilung vorkommt, sind gut untersucht. Wichtigster Fall ist das sogenannte Normalverteilungsmodell, in dem man von der Durchführung von  unabhängigen und normalverteilten Versuchen ausgeht. Dabei treten drei Fälle auf: 

• der Erwartungswert ist unbekannt und die Varianz bekannt
• die Varianz ist unbekannt und der Erwartungswert ist bekannt
• Erwartungswert und Varianz sind unbekannt.

Je nachdem, welcher dieser Fälle auftritt, ergeben sich verschiedene Schätzfunktionen, Konfidenzbereiche oder Tests. Diese sind detailliert im Hauptartikel Normalverteilungsmodell zusammengefasst. 

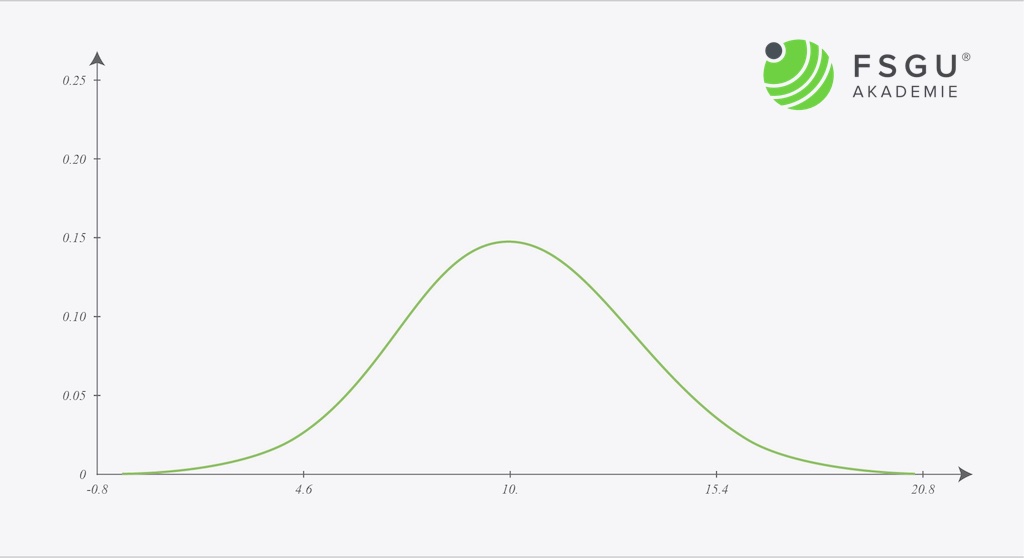
So sieht ein Beispiel für die Normalverteilung aus

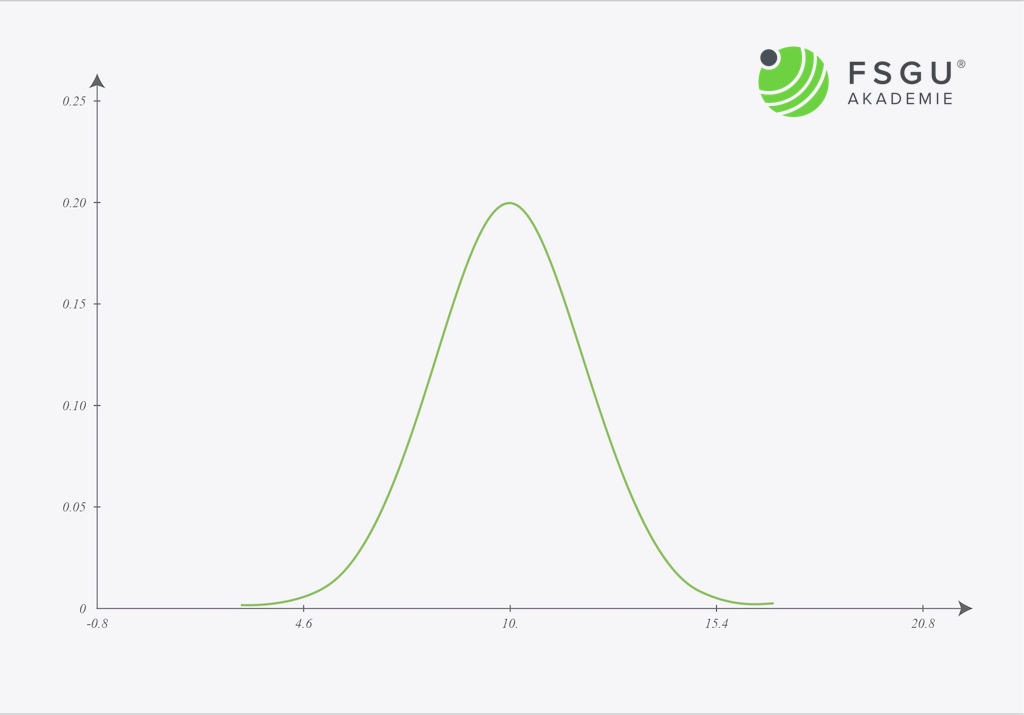
Um zu überprüfen, ob vorliegende Daten normalverteilt sind, können unter anderen folgende Methoden und Tests angewandt werden: 

• Chi-Quadrat-Test
• Kolmogorow-Smirnow-Test
• Anderson-Darling-Test (Modifikation des Kolmogorow-Smirnow-Tests)
• Lilliefors-Test (Modifikation des Kolmogorow-Smirnow-Tests)
• Cramér-von-Mises-Test
• Shapiro-Wilk-Test
• Jarque-Bera-Test
• Q-Q-Plot (deskriptive Überprüfung)
• Maximum-Likelihood-Methode (deskriptive Überprüfung)

Die Tests haben unterschiedliche Eigenschaften hinsichtlich der Art der Abweichungen von der Normalverteilung, die sie erkennen. So erkennt der Kolmogorov-Smirnov-Test Abweichungen in der Mitte der Verteilung eher als Abweichungen an den Rändern, während der Jarque-Bera-Test ziemlich sensibel auf stark abweichende Einzelwerte an den Rändern („heavy tails“) reagiert. 

Beim Lilliefors-Test muss im Gegensatz zum Kolmogorov-Smirnov-Test nicht standardisiert werden, d. h.,  und  der angenommenen Normalverteilung dürfen unbekannt sein. 

Mit Hilfe von Quantil-Quantil-Plots (auch Normal-Quantil-Plots oder kurz Q-Q-Plots) ist eine einfache grafische Überprüfung auf Normalverteilung möglich.
Mit der Maximum-Likelihood-Methode können die Parameter  und  der Normalverteilung geschätzt und die empirischen Daten mit der angepassten Normalverteilung grafisch verglichen werden. 

Was ist die weibull Verteilung?

Die Weibull Verteilung findet vor allem als Wahrscheinlichkeitsfunktion für die Lebensdauer-abschätzung Verwendung. Die Anwendungsmöglichkeiten sind vielfältig und reichen von Vorhersagen über Maschinen und Anlagenstandzeiten bis zu Versagensarten von verschiedenen metallischen und nichtmetallischen Werkstoffen („Wöhlerdiagramme“).

Die Wahrscheinlichkeitsfunktion der Weibull Verteilung ist mathematisch wie folgt beschrieben:

α….. Skalierungsparameter der Weibull Funktion 
β….. Formparameter der Weibull Funktion

Es gilt: α >0 und β > 0 

Durch die beiden Parameter α und β kann die Weibull Verteilung sowohl zur Darstellung von steigenden als auch fallenden Versagensraten herangezogen werden.

Die Exponentialverteilung ist ein Sonderfall der Weibull Verteilung und wird durch das Setzen des Formparameters β auf den Wert eins erreicht.

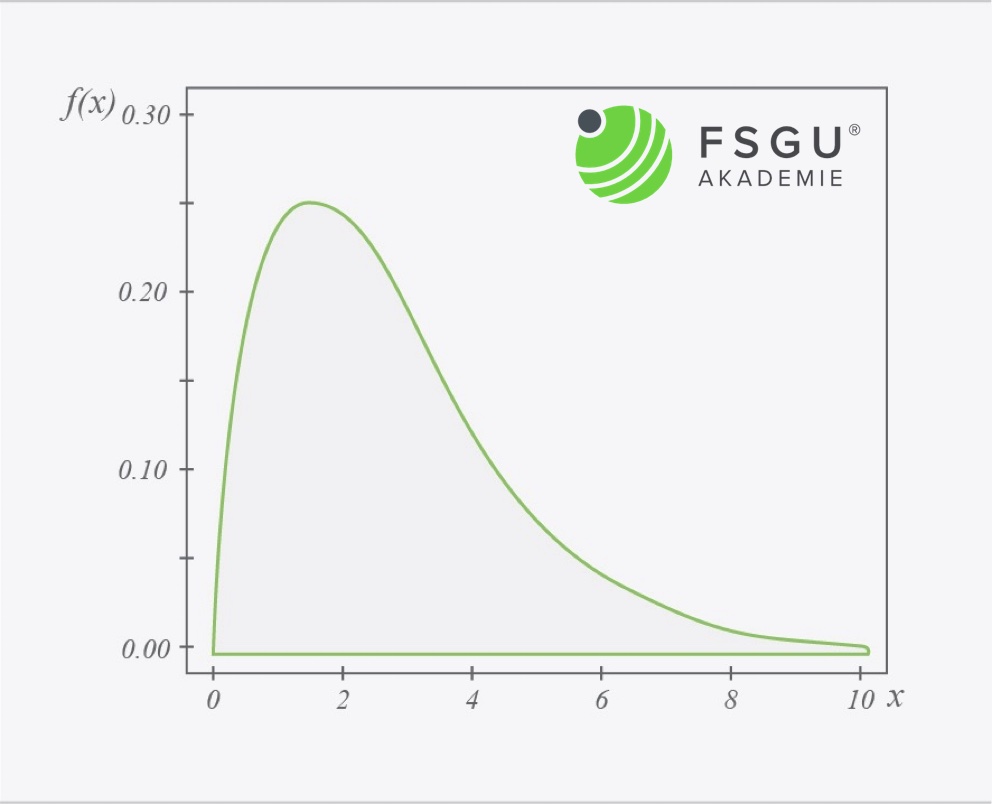
So sieht ein Beispiel für die weibull Verteilung aus

Die unten gezeigte Weibull Wahrscheinlichkeitsfunktion mit α =1,5 und β =3 stellt die durchschnittliche Lebensdauer von Standardglühbirnen dar.