Was ist Lagermanagement?

In einem Lager wird durch die Lagerhaltung der betriebliche Materialfluss unterbrochen. Hier werden bewusst Bestände gebildet. Man benötigt für die Lagerhaltung ein Lager, d. h. ein Gebäude, einen Raum oder ein Areal, in dem die Waren aufbewahrt werden können.

Die Lagerhaltung hat verschiedene Funktionen: Das Lager dient zum Beispiel als Pufferzone; das bedeutet, wenn die Beschaffungsmenge größer als die Produktionsmenge ist, wird das überflüssige Material für die Produktion als sogenannte Ausgleichsfunktion eingelagert. Schwankungen zwischen Einkaufs- und Verkaufsmarkt können mit dieser Funktion reduziert und ausgeglichen werden.

Die Ausgleichsfunktion wird durch die Bereitstellungsfunktion ergänzt, hier trägt die Bereitstellungs- bzw. Sortimentsfunktion bei der Lagerhaltung zu einer gewissen Kontinuität im Sortiment bei. Hier wird überbrückt, wenn bei Sortimenten Diskrepanzen zwischen Beschaffung und Verkaufsbedarfen entstanden sind.

Mittels der Sicherungsfunktion stellt das Lager die Produktion sicher. Hier geht es in erster Linie darum, dass die künftigen Mengenbedarfe sowohl in der Rohstoff-, Hilfsmittel- und Teilebeschaffung gedeckt sind, sogar, wenn die Daten auf Prognosen basieren, weil möglicherweise keine fundierten Bedarfsplanungen vorliegen. Beispiel hierfür sind Produkte, die saisonalen Schwankungen und/oder Lieferengpässen unterliegen.

Die Produktionsfunktion des Lagers wird auch als Veredelungsfunktion benannt, das bedeutet eine Weiterverarbeitung ist möglich. Die Veredelung tritt dann ein, wenn das Produkt durch Lagerung verändert / veredelt wird. Diese Lagerung ist Teil des Produktionsprozesses, beispielsweise bei der Reifung von Whiskey, Käse oder Wein.

Das Lagermanagement umfasst operative, taktische und strategische Aktivitäten in einem Lager. Diese Aktivitäten werden durch die Führungsebenen des Unternehmens in Auftrag gegeben. Sie dienen der Weiterentwicklung und der Erreichung der operativen und strategischen Unternehmensziele. Das Lagermanagement grenzt sich vom Logistikmanagement und Supply Chain Management in der Hinsicht ab, dass hier das System innerhalb der Gebäudegrenzen eines Lagers gemeint ist. 

Die Elemente des Lagermanagements sind:

• Inhalt: Lagerbereiche, Lagerprozesse
• Instrumente: Technik, Führung / Lagerorganisation (operativ)

Zur Lagertechnik zählen Lagersysteme, Bediengeräte und Informationstechnik. Lagerführung bzw. -organisation beschreibt die Art und Weise, wie die Lagerführung operativ organisiert wird und wie die Arbeiten prozessual verteilt und koordiniert werden.

Die Aufgaben des Lagermanagements liegen in der Konsolidierung und in der Abstimmung aller Zusammenhänge auf die oben beschriebenen Instrumente des Lagermanagements. Ziel des Lagermanagements ist es, nachstehende Zielgrößen zu erreichen:

• Betriebskosten (Lagerkosten)
• Lieferservice
• Umweltvorschriften
• Disponibilität

Professionelles Lagermanagement impliziert hohe Anforderungen, um die Logistik zeitgerecht, kostengünstig und souverän betreiben zu können. Kosteneffizienz und Kundenorientierung stehen neben dem günstigsten Grad der Auslastung und den Kapazitäten im Fokus eines modernen Lagermanagements.

Was sind die Grundlagen?

Der Begriff Lagern bedeutet per Definition die zielgerichtete Entsorgung vorgelagerter und die Versorgung nachgelagerter Arbeitsgänge mit Gütern. In einem Handelsbetrieb bedeutet lagern vor allem, die Lieferbereitschaft in Richtung Endverbraucher sicherzustellen.

Zur optimalen Beschaffung und Verwaltung von Gütern gibt es drei Beschaffungsarten, die im Rahmen  der Beschaffungs-Lagerplanung unterschieden werden sollen:

• die fallweise Beschaffung
• die fertigungssynchrone Beschaffung
• die Vorratsbeschaffung

Was ist das Prinzip der fallweisen Beschaffung?

Hier wird der Beschaffungsvorgang dann ausgelöst, wenn ein Bedarf festgestellt wird. Diese Anwendung kommt in der Praxis dann zum Tragen, wenn das Gut jederzeit und kurzfristig beschaffbar ist, das Gut sehr hochwertig ist und nicht regelmäßig genutzt wird oder der Bedarf des Materials aufgrund seiner Beschaffenheit nicht langfristig geplant werden kann. Beispielsweise in der auftragsorientierten Einzelfertigung wird nach diesem Prinzip verfahren. Das bedeutet nicht, dass in jeglicher Einzelfertigung immer dieses Prinzip angewendet wird, sondern die Anwendung bezieht sich in erster Linie auf Spezialteile und selten verwendete Teile. Standardisierte Güter und häufig verwendete Materialien werden auch in der Einzelfertigung bevorratet.

Was ist das Prinzip der fertigungssynchronen Beschaffung?

Bei der fertigungs- oder einsatzsynchronen Beschaffung erfolgt ein idealerweise lagerloser Zufluss des Materials. Dieses Prinzip wird auch Just-in-time-Beschaffung genannt. Die zeitliche und mengenmäßige Anpassung an den Verwendungsbedarf wird hier durch Prognosen und Simulationen so präzise vorgenommen, dass Einkaufslager überflüssig sind und sogar direkt bis in die Produktion geliefert werden kann (auch Just-in Sequence).

Was ist das Prinzip der Vorratsbeschaffung?

Bei der Vorratsbeschaffung werden für die verschiedenen Güter Eingangslager einbezogen. Die Anwendung dieses Prinzips kommt hauptsächlich zum Einsatz, wenn ein zufallsbedingter Bedarfsverlauf vorliegt (= stochastische Bedarfsverläufe), während bei der fertigungssynchronen und auch bei der fallweisen Beschaffung notwendigerweise eine deterministische, das heißt genau festgelegte Bedarfsstruktur zu Grunde liegt. Bei der deterministischen Bedarfsstruktur können aufgrund der bekannten Beschaffungszeiten die jeweiligen Bestellmengen und -zeitpunkte direkt aus der Bedarfsplanung verwendet und abgeleitet werden. Die Höhe des Lagerbestandes muss mit den Einflussfaktoren (Verfall, Kapitalbindung, Platzmangel) der Vorratshaltung abgeglichen werden.

Bei der Lagerhaltung gibt es unterschiedliche Lagerverfahren und -strategien. Zum einen gibt es das Fifo-Prinzip (First In – First Out), bei dem die Waren, die zuerst eingelagert worden sind, zuerst wieder ausgelagert werden. Somit verhindert man „Ladenhüter“. Das Fifo-Prinzip ist eigentlich die gängigste Strategie.

Zum anderen gibt es das Lifo-Prinzip (Last In – First Out), bei dem erst die zuletzt eingelagerten Vorräte aus dem Lager entnommen werden. Dies ist eher unüblich, jedoch oft eine zwangsläufige Konsequenz aus der Lagerkonstruktion oder der Eingangssituation besonders in Spitzenzeiten. 

Auslagerungen nach dem Mindesthaltbarkeitsdatum findet man beispielsweise im Lebensmittelbereich mit dem FEFO-Prinzip, First Expire – First Out).

Eine eher untergeordnete Rolle spielen andere Lagerstrategien wie beispielsweise das Hifo-Prinzip (Highest In – First Out) oder das Lofo-Prinzip (Lowest In – First Out).

Was ist Bestandsmanagement?

Beim Bestandsmanagement geht es um die Reduzierung der Lagerbestände; gleichzeitig muss eine Erhöhung oder Erhaltung des Lieferservices gewährleistet sein. Mit dem zuverlässigen Lieferservice steigt die Kundenzufriedenheit bis hin zum Ausbau der Geschäftstätigkeit eben weil der Lieferservice signifikant ansteigt. Das Bestandsmanagement erfolgt aufgrund von artikelspezifischen Planungsstrategien in drei Prozessschritten: Bedarfs-, Bestands- und Beschaffungsplanung.

Was ist Bedarfsplanung?

Die Bedarfsplanung ermittelt den künftigen Bedarf. Hier werden zwei Verfahren unterschieden: a) verbrauchsgebundene Bedarfsplanung und b) programmgebundene Bedarfsplanung. Grundlage für die verbrauchsgebundene Bedarfsplanung schafft ein Prognoseverfahren, das mit dem periodisierten Verbrauch und somit mit historischen Daten durchgeführt wird. Die Basis für programmgebundene Bedarfsplanung liegt in der konkreten Analyse und Planung der vorliegenden Kundenaufträge.

Außerdem muss zwischen der Termin- und Mengenplanung unterschieden werden. Der Bedarfstermin, der auf der Vorwärts- oder Rückwärtsterminrechnung basiert, wird durch ein ERP-System ausgewiesen. Wenn die konkrete Terminbestimmung gelten soll, wird im Nachgang die Bedarfsmenge errechnet. Dabei wird die rechnerische Bedarfsmenge über das Verfahren der Losgrößenberechnung angepasst. Man kann die Losgröße auch noch über die sog. Rundungswerte (z. B. Einheit, volle Palette) oder Mindestbestellwerte bzw. -mengen zu dem Lieferanten verändern.

Periodisch werden die Bedarfsmengen erfasst und optimiert zu einer einzigen Losgröße zusammengeführt, wobei hier zwischen den Lagerhaltungskosten und losgrößenfixen Kosten ein Kostenoptimum ermittelt werden muss. Es gibt folgende optimierende Verfahren in der Losgrößenberechnung: Zum einen gibt es die klassische Losformel, die man auch unter den Namen Andlersche Losgröße beziehungsweise Harris–Formel kennt, und zum anderen gibt es die dynamische Losgrößenermittlung (zum Beispiel nach Heuristiken, Groff sowie die statistische Losgrößenermittlung).

Losgröße ist ein Begriff aus der Fertigungstechnik und diese gibt die Menge eines Gebindes an. Gebinde bedeutet hier einer Charge, Sorte oder Serie, die hintereinander ohne Umschaltung oder Unterbrechung der Fertigung hergestellt worden ist. Als Charge bezeichnet man die Menge eines Erzeugnisses, die unter einheitlichen Bedingungen entstanden ist.

Ein Los (lot) ist die Menge eines Produktes, die ohne Unterbrechung gefertigt wird und die Losgröße (lotsize) der Umfang des Loses. Bei der Losgrößenplanung (lotsizing) stellt sich die Frage, ob Produktionsmengen zu größeren Losen zusammengefasst werden sollen, um Rüstkosten zu sparen. Bei einer Zusammenfassung zu größeren Losen können die Bestände als Vorproduktion für spätere Perioden auf Lager gelegt werden. Dadurch werden zwar Rüstkosten gespart, aber es entstehen zusätzliche Lagerkosten.

Bei Losgrößen- bzw. Lagerhaltungsmodellen unterscheidet man deterministische Modelle (bei bekannter Nachfrage) im Gegensatz zu stochastischen Modellen (nur Wahrscheinlichkeitsverteilungen über die Nachfragemengen bekannt) sowie statische Modelle (konstante Nachfrage – eine typische Bestellperiode) und dynamische Modelle (Nachfrage variiert mit der Zeit).

Eine weitere Unterscheidung erfolgt in Ein-Produktmodelle und Mehr-Produktmodelle, hier muss weiter unterschieden werden zwischen Mehr-Produktmodellen mit unabhängigem Bedarf (Kapazitätsbeschränkung) und Mehr-Produktmodellen mit abhängigem Bedarf (Halbfertigprodukte nur in der mehrstufigen Produktion).

Was ist deterministische Losgrößenmodelle?

Bei deterministischen Ein-Produktmodellen betrachtet man nur ein Produkt. Bei Herstellung mehrerer Produkte nimmt man an, dass die Bedarfsmengen unabhängig voneinander sind. Die Situation kann durch mehrere unabhängige Einprodukt-Lagerhaltungsmodelle beschrieben werden. 

Ein erster Ansatz zur Bestimmung der optimalen Bestellmenge ist das klassische Losgrößenmodell, das zur Losgrößenplanung dient. Bei der klassischen Losgrößenformel, auch Andlersche Bestellmengenformel genannt, wird von einem hohen, regelmäßigen, kontinuierlichen Bedarf mit einer konstanten Bedarfsrate (stationärer Bedarf) ausgegangen. Dadurch entspricht die durchschnittliche Anzahl an Bestellungen bzw. Losauflagen pro Zeiteinheit dem Quotienten aus Bedarfsrate und Bestellmenge bzw. Losgröße.

Gesetzt den Fall, ein schneller Lagerzugang wird angenommen, so ist der durchschnittliche Lagerbestand in einer zeitkontinuierlichen Betrachtung der halben Bestellmenge bzw. Losgröße zu planen. Die optimale Losgröße errechnet sich als Wurzel aus der doppelten Bedarfsrate multipliziert mit den fixen Kosten einer Bestellung bzw. einer Losauflage (Rüstkosten), geteilt durch den Lagerkostensatz. Daher stammt auch die Bezeichnung der klassischen Bestellmengen- bzw. Losgrößenformel als „Wurzelformel“.

Diese Situation ist bei gemeinsamen Kapazitätsbeschränkungen und/oder bei mehrstufiger Produktion oft nicht gegeben.

Was sind deterministische dynamische Modelle?

Beim mehrstufigen unkapazitierten Losgrößenproblem geht man von folgenden Grundannahmen aus:

Man unterstellt einen endlichen Planungshorizont (T Perioden) und n (Vor-)Produkte bei einer mehrstufigen Produktstruktur. Eine zeitlich veränderliche (dynamische) Primärnachfrage gibt es nur für das Endprodukt n. Fertigungsgeschwindigkeiten werden als unendlich angesehen, es existieren keine Kapazitätsbeschränkungen.

Zudem geht man von fixen Rüstkosten, unveränderlichen variable Fertigungskosten und linearen Lagerhaltungskosten je Produkt aus, die im Planungszeitraum unveränderlich sind. Fehlmengen sind nicht vorgesehen. Ein Beispiel wäre die Herstellung eines Stuhls. Dazu sind n=7 Teile notwendig, 4 Stuhlbeine, eine Lehne und der Sitz, was schließlich im siebten Teil, dem Stuhl mündet. 

Was sind stochastische Modelle?

Bei stochastischen Losgrößenmodellen erfolgt auch eine Berücksichtigung von Unsicherheiten. Gewisse Problemparameter beschreibt man über Zufallsvariablen, hierzu zählen zum Beispiel Nachfrage, Lieferfristen, Fertigungsgeschwindigkeiten (zum Beispiel Ausfälle).

Das Problem liegt in der Ermittlung adäquater Wahrscheinlichkeitsverteilungen. Klassifikationsmerkmale deterministischer Losgrößenmodelle sind prinzipiell auch auf stochastische Losgrößenmodelle anwendbar. Es erfolgt häufig eine Einschränkung auf Einproduktmodelle.

In der Unternehmensrealität sind die Daten, hier sind die Nachfragedaten gemeint, nicht mit Sicherheit bekannt. In der Planungspraxis versucht man, dies zu berücksichtigen, zum Beispiel indem bei der Nettobedarfsrechnung der verfügbare Lagerbestand um einen Sicherheitsbestand angepasst wird und dann die Losgrößen mit einem Losgrößenmodell für deterministischen Bedarf, zum Beispiel dem heuristischen Silver-Meal-Verfahren, oder mit dem exakten Verfahren bestimmt werden. Als problematisch erweist sich hierbei, dass oftmals auf eine unbekannte Größe gestoßen wird: Die richtige Höhe des Sicherheitsbestandes. Der Sicherheitsbestand ist immer abhängig von der Länge der Beschaffungszeit und des Nachfragebedarfes, also davon, wie die Wahrscheinlichkeitsverteilung der Nachfragemenge im Risikozeitraum liegt.

„Darüber hinaus wird der Sicherheitsbestand von der Losgröße beeinflusst. In Abhängigkeit vom angestrebten Servicegrad kann es auch erforderlich sein, einen negativen Sicherheitsbestand einzuplanen. Nehmen wir zum Beispiel an, es wird eine möglichst optimale Lagerpolitik mit kontinuierlicher Bestandsüberwachung verfolgt. Die Periodennachfragemenge sei mit dem Mittelwert 100 und der Standardabweichung 30 normalverteilt. Die Wiederbeschaffungszeit ist deterministisch und beträgt 14 Tage. Bei einer Losgröße von 1000 und einem angestrebten ß-Servicegrad von 99% beträgt der optimale Sicherheitsbestand 108.25.“

Für die Bestimmung des Sicherheitsbestands muss die Losgröße bekannt sein. Das bedeutet, sowohl die Losgröße als auch der Sicherheitsbestand müssen gleichzeitig festgelegt werden. In einem stochastischen Losgrößenmodell wird nun explizit berücksichtigt, dass die Höhe des Sicherheitsbestands nicht ein extern festgelegtes Datum ist, sondern unmittelbar von der Losgröße abhängt. In einem solchen Modell wird mit der Entscheidung über eine Losgröße gleichzeitig implizit der Sicherheitsbestand festgelegt.

Es gibt außer dem Fall der deterministischen Nachfrage wenige Ansätze zur Losgrößenplanung unter stochastischen Bedingungen. Die stochastischen Losgrößenmodelle lassen sich danach unterscheiden, ob sie in der Zielfunktion Fehlbestandskosten berücksichtigen oder ob sie auf diese schwer quantifizierbaren Größen verzichten und stattdessen eine Servicegrad-Nebenbedingung berücksichtigen.

In der Praxis dient die Losgrößenplanung der Ausschöpfung von organisatorischen und technischen Maßnahmen zur Reduktion des Rüstaufwands. Hierzu bedient man sich problemadäquater Losgrößenmodelle unterstützt durch Verfahren der Forschung. Eine realistische Darstellung kann mittels betriebswirtschaftlicher Standardsoftware erfolgen.

Die Losgrößenplanung erfährt eine Einordnung in übergeordnete Koordinationsprobleme wie den hierarchischen Planungsprozess bzw. dezentrale Koordination. Gleichzeitig müssen die Bereiche Produktion und Distribution sowie das Supply Chain Management einbezogen werden.

Was ist Bestandsplanung?

In der Bestandsplanung werden die notwendigen Bestände bestimmt und festgelegt. Es wird sowohl der optimale Sicherheitsbestand als auch der Bestellauslösebestand ermittelt. Weiterhin bestehen Höchst- und Maximalbestände, bei denen es aufgrund der Lagerrestriktionen (Auslastungsgrad, Sicherheitsvorkehrungen) keine Überschreitung geben darf.

Was ist Beschaffungsplanung?

In der Beschaffungsplanung wird die Bestellpolitik festgelegt. In Abhängigkeit der Bestellpolitik wählt man den entsprechenden Bestellzeitpunkt nach den Merkmalen der Artikel aus. Außerdem wird die optimale Bestellmenge mit einem passenden heuristischen bzw. optimierenden Verfahren artikelspezifisch ermittelt.

Ein Beispiel für die Beschaffungsplanung ist das Bestellpunktverfahren.

Was ist das Bestellpunktverfahren?

Als Bestellpunktverfahren wird ein Verfahren benannt, das zur Bestimmung von Bestellzeitpunkt und Bestellmenge in der Lagerhaltung eingesetzt wird. Durch die Anwendung des Bestellpunktsystems wird sichergestellt, dass immer dann Ware im Lager verfügbar ist, wenn sie benötigt wird. Das Bestellpunktsystem ist ein Teilbereich der Bestellpolitik. Es gehört zu den verbrauchsorientierten Bestellverfahren, die in Bestellpunktsystem und Bestellrhythmussystem unterteilt werden können.

Die folgende Darstellung zeigt den optimalen Bestellzeitpunkt:

Die Bestimmung der optimalen Bestellmenge wird mit der Andler-Formel vorgenommen. Hier sollen zwei Fragestellungen beantwortet werden: Wie hoch ist die optimale Bestellmenge und wann ist der optimale Bestellzeitpunkt? 

Nachfolgend die Erläuterung der Andlerschen Bestellmengenformel:

Gegeben sind:

• Jahresbedarfsmenge m
• Bestellkosten E (fixe Kosten pro Bestellung)
• der Einstandspreis p (Kaufpreis je Mengeneinheit)
• Lagerhaltungskostensatz s (ein Prozentsatz vom Lagerwert, als Summe eines Zinssatzes für das gebundene Kapital und den Lagerkostensatz)
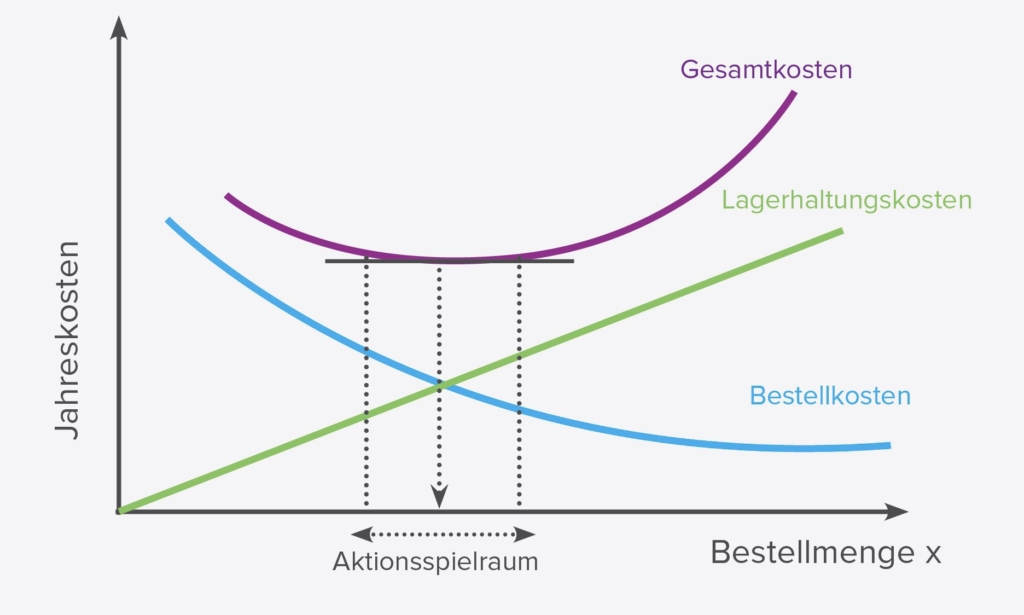
• gesucht ist die optimale Bestellmenge x_opt, bei der die Summe von Bestell- und Lagerkosten minimal ist

Modellprämissen des Grundmodells der optimalen Bestellpolitik sind ein konstanter Verbrauch und eine konstante Lieferdauer, die Annahme bestellfixer Kosten sowie die Annahme linearer Lager- und Kapitalbindungskosten.

Bei einer Jahresbedarfsmenge m und einer Bestellmenge x sind Bestellungen erforderlich, jede verursacht Kosten von E.

Die Bestellkosten sind

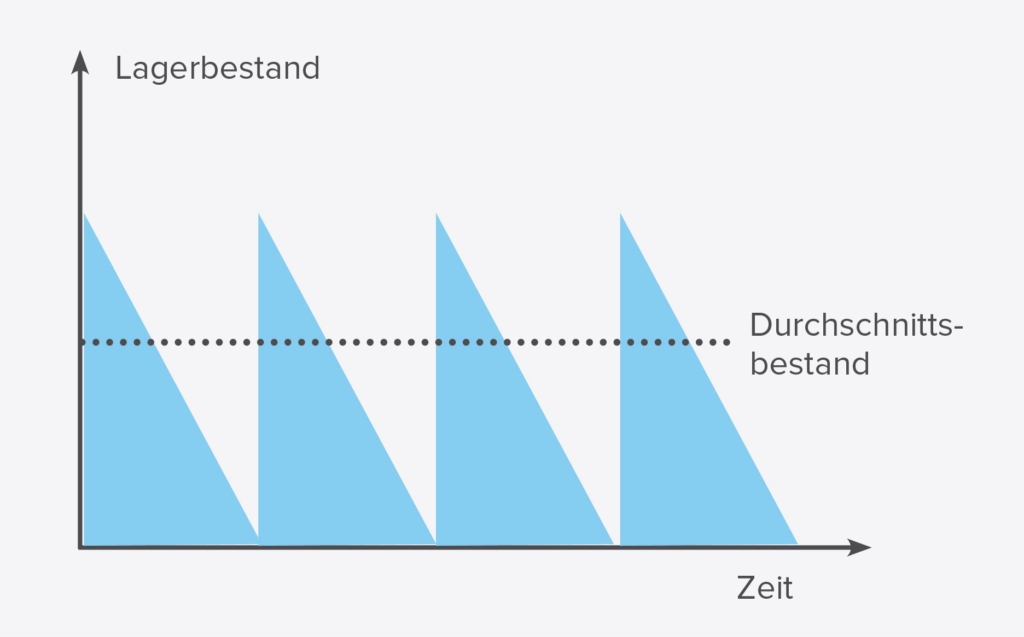
Vorgesetzt wird, dass der Lagerabgang mit konstanter Rate erfolgt und dass die neue Lieferung (von x Mengeneinheiten) dann eintrifft, wenn der Lagerbestand bei 0 ist. Der Lagerbestand hat somit einen sägezahnförmigen Verlauf über der Zeit und im Mittel ergibt sich somit der durchschnittliche Lagerbestand. Der durchschnittliche Wert des Lagerbestands ist somit: Maximaler Lagerbestand geteilt durch 2.

Die Lagerkosten K_L betragen mithin

Die Gesamtkosten K_G ergeben sich wie folgt:

Die Kosten sind dann minimal, wenn die Bedingung 1. Ordnung erfüllt ist:

Obige Formel wird nach x aufgelöst und man findet die Andlersche Formel für die optimale Bestellmenge:

Diese Formel ist in zwei Variationen in der Literatur zu finden: Wenn die Lagerhaltungskosten mit 0,05% gewertet werden, dann nimmt man den Multiplikator 2 anstatt 200, werden die Lagerhaltungskosten mit 5% angesetzt, bleibt die 200.

Es sind jedoch Einschränkungen in der Anwendung der Formel zu beachten. Sie greift nur bei konstanter und bekannter Bedarfsmenge und berücksichtigt keine Mindest- oder Höchstmengen. Auch die Preise/Kosten für das Beschaffungsgut und die Lagerkosten bleiben konstant und mengenunabhängig. Die Lieferzeit ist Null und es wird mit einem kontinuierlichen Lagerabgang kalkuliert.

Wie bereits erläutert, setzt die Andler-Formel den Bezug zwischen Lagerhaltungskosten, Zinsen für das eingelagerte Material, die Stückkosten mit Mengenrabatten und die Beschaffungsfixkosten (zum Beispiel: Porto, Versand und Verpackung) und den Jahresbedarf zueinander in Relation, um aus diesen Werten die kostengünstigste Bestellmenge und -häufigkeit herauszufinden.

Beispiel:
Ein Unternehmen hat mittelbare Beschaffungskosten von 30,00 € für eine Mengeneinheit (ME) einer Ware, der Lagerhaltungskostensatz beträgt 15%; der Gesamtbedarf liegt bei 1250 ME p.a., der Einführungspreis pro ME (Neueinführung am Markt) beträgt 20,00 €. Ermitteln Sie die optimale Bestellmenge.

Aus der obigen Aufgabe ergibt sich folgende Ausgangslage:

m = Gesamtbedarf = 1.250 ME
E = Bestellkosten = 30,00 €
p = Einstandspreis = 20,00 €
s = Lagerzinssatz = 15% 

Andlersche Formel zur Bestimmung der optimalen Bestellmenge: 

daraus folgt: 

Die optimale Bestellmenge im obigen Beispiel beträgt also in etwa 159 ME.